Missing data¶
- Values in a data set may be missing. This leaves us unable to fit a model or perform other useful strategies to the dataset. Missing data tends to introduce bias that leads to misleading results so they cannot be ignored. (Filling missing values by testing which impacts the variance of a given dataset the least is the best approach.)
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
Data¶
- Titanic Dataset: Build a predictive model that answers the question: “what sorts of people were more likely to survive?” using passenger data (ie name, age, gender, socio-economic class, etc). This data was collected after the accident.
url = 'https://raw.githubusercontent.com/krishnaik06/Feature-Engineering-Live-sessions/master/titanic.csv'
df = pd.read_csv(url)
df.info()
df.head()
What are the different types of Missing Data?¶
- Missing Data Not At Random(MNAR): Systematic missing Values There is absolutely some relationship between the data missing and any other values, observed or missing, within the dataset.
df.isnull().sum()
- Is there a relationship between
AgeandCabin? Yes, when we gave the survey all details were available outside of first age because the data was taken after the crash so that person would be dead so noAgecould be recorded.The second variableCabinif the passenger is dead they also cannot give any cabin information. So theAgeandCabinvariables are MNAR.
Missingo heatmap¶
- The missingno correlation heatmap measures nullity correlation: how strongly the presence or absence of one variable affects the presence of another. Nullity correlation ranges from -1 (if one variable appears the other definitely does not) to 0 (variables appearing or not appearing have no effect on one another) to 1 (if one variable appears the other definitely also does). Entries marked $<1$ or $<-1$ have a correlation that is close to being exactingly negative or positive, but is still not quite perfectly so. This points to a small number of records in the dataset which are erroneous.
import missingno as msno
msno.heatmap(df, cmap='viridis')
b, t = plt.ylim()
b += 0.5
t -= 0.5
plt.ylim(b, t)
plt.show();
Missingo dendrogram¶
- The dendrogram allows you to more fully correlate variable completion, revealing trends deeper than the pairwise ones visible in the correlation heatmap. The dendrogram uses a hierarchical clustering algorithm (courtesy of scipy) to bin variables against one another by their nullity correlation (measured in terms of binary distance). At each step of the tree the variables are split up based on which combination minimizes the distance of the remaining clusters. The more monotone the set of variables, the closer their total distance is to zero, and the closer their average distance (the y-axis) is to zero. To interpret this graph, read it from a top-down perspective. Cluster leaves which linked together at a distance of zero fully predict one another's presence—one variable might always be empty when another is filled, or they might always both be filled or both empty, and so on. In this specific example the dendrogram glues together the variables which are required and therefore present in every record.
msno.dendrogram(df);
- Missing Completely at Random, MCAR: A variable is missing completely at random (MCAR) if the probability of being missing is the same for all the observations. When data is MCAR, there is absolutely no relationship between the data missing and any other values, observed or missing, within the dataset. In other words, those missing data points are a random subset of the data. There is nothing systematic going on that makes some data more likely to be missing than other.
df[df['Embarked'].isnull()]
- The
Embarkedvariable is which station the passengers where picked up and dropped off at. This variable is MCAR bothAgeandCabinare present
Missingo matrix¶
- A nullity matrix is a data-dense display which lets you quickly visually pick out patterns in data completion. The sparkline at right summarizes the general shape of the data completeness and points out the rows with the maximum and minimum nullity in the dataset. This visualization will comfortably accommodate up to 50 labelled variables. Past that range labels begin to overlap or become unreadable, and by default large displays omit them.
import missingno as msno
msno.matrix(df);
- Missing Data Not At Random(MNAR): Systematic missing Values There is absolutely some relationship between the data missing and any other values, observed or missing, within the dataset.
# Percentage of missing values
df.isnull().mean()
# Binary transform if cabin is present or not
df['cabin_null'] = np.where(df['Cabin'].isnull(),1,0)
# Find percent of missing cabin values for survivers and non survivers
df.groupby(['Survived'])['cabin_null'].mean()
- Missing At Random(MAR): Missing at Random means the propensity for a data point to be missing is not related to the missing data, but it is related to some of the observed data.
- Whether or not someone answered #13 on your survey has nothing to do with the missing values, but it does have to do with the values of some other variable.
- The idea is, if we can control for this conditional variable, we can get a random subset. Good techniques for data that is missing at random need to incorporate variables that are related to the missingness.
All the techniques of handling missing values¶
- Mean, Median, Mode replacement
- Random Sample Imputation
- Capturing NAN values with a new feature
- End of distribution imputation
- Arbitrary imputation
- Frequent categories imputation
- Forward and backward filling
- Estimator imputation
How To Handle Continuous and Discrete Continuous Missing Values¶
Mean, Median, Mode imputation¶
- When should we apply? Mean, median, mode imputation has the assumption that the data are missing completely at random (MCAR). We solve this by replacing the NAN with the most frequent occurrence of the variable.
df = df[['Age','Fare','Survived']]
df.head()
# Percentage of missing values
df.isnull().mean()
# Function to impute with a fillna method
def impute_nan(df=df,variable='Age',strat=None, method=None):
df[variable + "_" + method]=df[variable].fillna(strat)
methods = [df.Age.mean(), df.Age.median(), df.Age.mode()]
names = ['mean', 'median', 'mode']
for m, name in zip(methods, names):
type_ = int(m)
impute_nan(df,'Age', type_, method=name)
df.head()
Median is more robust to outliers, if the dataset has outliers using the mean could affect the analysis.
age_cols = [x for x in list(df.columns) if 'Age' in x]
for col in age_cols:
df[col].plot(kind='kde', label=f'{col}, std = {round(df[col].std(),3)}')
plt.legend()
plt.show()
Advantages And Disadvantages of Mean, Median, Mode Imputation¶
Advantages
- Easy to implement(robust to outliers)
- Faster way to obtain the complete dataset
Disadvantages
- Change or Distortion in the original variance
- Impacts Correlation
Random Sample Imputation¶
- Random sample imputation consists of taking random observation from the dataset and we use these random observations to replace the NaN values. This method assumes that the data are missing completely at random (MCAR).
# Generate a random sample from Age without missing values of the same length as the missing values
sample = df['Age'].dropna().sample(df['Age'].isnull().sum(), random_state=0)
print('# of samples', len(sample))
sample.head()
def impute_random(df, variable):
df[variable + "_random"] = df[variable]
# Create the random sample to fill the NaNs
random_sample = df[variable].dropna().sample(df[variable].isnull().sum(), random_state=0)
# Pandas needs the same index in order to find and fill the NaN locations
random_sample.index = df[df[variable].isnull()].index
# New column without NaNs filled by random sample
df.loc[df[variable].isnull(),variable+'_random']=random_sample
impute_random(df,"Age")
df.info()
df.head()
age_cols = ['Age', 'Age_mode', 'Age_random']
for col in age_cols:
df[col].plot(kind='kde', label=f'{col}, std = {round(df[col].std(),3)}')
plt.legend()
plt.show()
The random sample imputation actually matches the original distribution the best with the least distortion in variance
Random Sample Imputation Advantages and Disadvantage¶
Advantages
- Easy To implement
- There is less distortion in variance
Disadvantages
- Every situation randomness wont work
Capturing NaN values with a new feature¶
It works well if the data are not missing completely at random but show charateristics of Missing Data Not At Random (MNAR). This also works for categorical data.
# Create a feature that is a binary representation of its preseance
df['Age_NAN'] = np.where(df['Age'].isnull(), 1, 0)
df.head()
Capturing NaN values with a new feature Advantages and Disadvantages¶
Advantages
- Easy to implement
- Captures the importance of missing values
Disadvantages
- Creating Additional Features (curse of dimensionality)
End of Distribution imputation¶
If there is suspicion that the missing value is not MAR or MCAR then capturing that information is important. In this case, one would want to replace missing data with values that are at the tails of the distribution of the variable.
- If normally distributed, we use the mean +/- $3$ times Standard Deviation.
- If the distribution is skewed, use the IQR proximity rule.
df.Age.hist(bins=50);
sns.boxplot('Age',data=df);
Outliers only exist in the extreme
# Get extreme values from distribution
extreme = df.Age.mean() + (3 * df.Age.std())
print(f'Extreme = {extreme}')
df.loc[np.where(df['Age'] >= extreme)]
def impute_extreme(df, variable, extreme):
df[variable + "_end_dist"]=df[variable].fillna(extreme)
impute_extreme(df,'Age', extreme)
df.head()
age_cols = ['Age', 'Age_mode', 'Age_random', 'Age_end_dist']
for col in age_cols:
df[col].plot(kind='kde', label=f'{col}, std = {round(df[col].std(),3)}')
plt.legend()
plt.show()
plt.figure(figsize=(12,5))
plt.subplot(121)
sns.boxplot('Age', data=df)
plt.title('Age')
plt.subplot(122)
sns.boxplot('Age_end_dist', data=df)
plt.title('Age_end_dist')
plt.show()
End of Distribution imputation Advantages and Disadvantages¶
Advantages
- Easy to implement
- Can bring out the importance of missing values.
Disadvantages
- Can distort variance
- If there are many NaNs it will mask true outliers in the distribution
- If there are few NaNs the replaced NaNs may be considered an outlier and be pre-processed in a subsequent task of feature engineering.
Dropping all columns or rows¶
This works best when there are a very small number of missing values.
- Dropping all columns removes any variable that has any missing data
- Dropping all rows removes all missing data from all columns
# create missing values df
data = [ ('D',1,10,6,np.NaN),
('D',2,12,10,12),
('X',1,28,15,np.NaN),
('D',3,np.NaN,4,np.NaN),
('X',2,np.NaN,20,25),
('X',3,32,31,25),
('T',1,220,250,np.NaN),
('X',4,30,22,np.NaN),
('T',2,240,170,np.NaN),
('X',2,38,27,np.NaN),
('T',3,np.NaN,44,np.NaN),
('D',1,20,18,80),
('D',4,200,120,150)]
labels = ['item1', 'month','normal_price','item2','final_price']
df = pd.DataFrame.from_records(data, columns=labels)
df.info()
df
# Removing all rows
df.dropna(axis=0)
# Removing all columns
df.dropna(axis=1)
Dropping all columns or rows Advantages and Disadvantages¶
Advantages
- Easy to implement
- Cleans the entire dataset
Disadvantages
- Only works for a very small number of missing values
- Can loose a lot of useful information by removing data completely
Forward and Backward filling¶
Filling in missing data with its next or previous value. This works specifically when we know the missing data recorded is missing but unchanged.
- Problem: I want to fill NaN in the
normal_price,final_pricecolumns for each item with the 'normal_price','final_price' of its preceding month (if not available by its succeeding month).
# Chain together bfill and ffill to then fill the remaining NaN values:
df.ffill().bfill()
Forward and Backward filling Advantages and Disadvantages¶
Advantages
- Easy to implement
- Cleans entire dataset
Disadvantages
- May remove a ton of useful information
- Only works with very few missing values
- Only works with very few use cases
How To Handle Categroical Missing Values¶
Frequent Category Imputation¶
With this method you impute missing data with the most frequently occurring value. This method would be best suited for categorical data, as missing values have the highest probability of being the most frequently occurring value.
- Assumptions: Data is missing at random MAR; missing values look like majority.
Dataset¶
- Kaggle House prices dataset: Dataset of various attributes of a house to predict its price
url_train = 'https://raw.githubusercontent.com/liyenhsu/Kaggle-House-Prices/master/data/train.csv'
df = pd.read_csv(url_train, usecols=['BsmtQual','FireplaceQu','GarageType','SalePrice'])
df.info()
df.isnull().sum()
df.isnull().mean().sort_values(ascending=True)
Compute the frequency of each every feature¶
fig, ax = plt.subplots(nrows=1, ncols=3, figsize=(12,5))
df['BsmtQual'].value_counts().plot.bar(ax=ax[0])
df['GarageType'].value_counts().plot.bar(ax=ax[1])
df['FireplaceQu'].value_counts().plot.bar(ax=ax[2])
ax[0].set_title('BsmtQual')
ax[1].set_title('GarageType')
ax[2].set_title('FireplaceQu')
plt.tight_layout()
plt.show()
def impute_mode_cat(df, variable):
most_frequent_category = df[variable].dropna().mode()[0]
#print(most_frequent_category)
df[variable + '_mode'] = df[variable]
df[variable + '_mode'].fillna(most_frequent_category, inplace=True)
for feature in ['BsmtQual','FireplaceQu','GarageType']:
impute_mode_cat(df, feature)
df.head()
df.isnull().mean()
Frequent Category Imputation Advantages and Disadvantages¶
Advantages
- Easy to implement
- Suitable for categorical data
Disadvantages
- May create a biased data-set, favoring most frequent value , if there are many NaNs
- It distorts the relationship of the most frequent label
Arbitrary Value Imputation¶
Here, the purpose is to flag missing values in the data set. You would impute the missing data with a fixed arbitrary value (a random value).
It is mostly used for categorical variables, but
can also be used for numeric variableswith arbitrary values such as $0$, $999$ or other similar combinations of numbers.
def impute_new_cat(df, variable):
df[variable + "_newvar"] = np.where(df[variable].isnull(), "Missing", df[variable])
for feature in ['BsmtQual','FireplaceQu','GarageType']:
impute_new_cat(df, feature)
df.head()
Arbitrary Value Imputation¶
Advantages
- Easy to implement
- Captures the importance of missingess if there is importance
Disadvantages
- Distorts the original distribution of the variable
- If missingess is not important, it may mask the predictive power of the original variable by distorting its distribution
- Hard to decide which value to use
Filling Missing Values With a Model¶
For this we can use scikit learns IterativeImputer. This models each feature with missing values as a function of other features, and uses that estimate for imputation. It does so in an iterated round-robin fashion: at each step, a feature column is designated as output $y$ and the other feature columns are treated as inputs $X$. A regressor (BayesianRidge(), ExtraTreesRegressor()) is fit on ($X$, $y$) for known $y$. Then, the regressor is used to predict the missing values of $y$. This is done for each feature in an iterative fashion, and then is repeated for max_iter imputation rounds.
# create missing values df
data = [ (np.NaN, 'A', 1,10,6,np.NaN),
('D', 'D', 2,12,10,12),
('X', np.NaN, 1,28,15,np.NaN),
('D', 'D', 3,np.NaN,4,np.NaN),
('X', 'B', 2,np.NaN,20,25),
(np.NaN, 'B', 3,32,31,25),
('T', 'F', 1,220,250,np.NaN),
('X', np.NaN, 4,30,22,np.NaN),
('T', np.NaN, 2,240,170,np.NaN),
('X', 'C', 2,38,27,np.NaN),
('T', 'C', 3,np.NaN,44,np.NaN),
(np.NaN, 'A', 4,20,18,80),
('D', np.NaN, 4,200,120,150)]
labels = ['item1', 'grade', 'month','normal_price','item2','final_price']
df = pd.DataFrame.from_records(data, columns=labels)
df.info()
df_ = df.copy()
df
from sklearn import preprocessing
import warnings
warnings.filterwarnings('ignore')
encoder = preprocessing.OrdinalEncoder()
cat_cols = ['item1','grade']
# Function to encode non-null data and replace it in the original data'
def encode(data):
# Retains only non-null values
nonulls = np.array(data.dropna())
# Reshapes the data for encoding
impute_reshape = nonulls.reshape(-1,1)
# Encode data
impute_ordinal = encoder.fit_transform(impute_reshape)
# Assign back encoded values to non-null values
data.loc[data.notnull()] = np.squeeze(impute_ordinal)
return data
for columns in cat_cols:
encode(df[columns])
print('\nOriginal:', '\n', df_)
print('\nEncoded:', '\n',df)
Imputation Using Deep Learning:¶
This method works very well with categorical and non-numerical features. For this we use a keras scikit learn wrapper to use a deep learning model as a scikit learn classifier or regressor.
Pros:
- Quite accurate compared to other methods.
- It supports continuous and categorical data.
Cons:
- Can be quite slow with large datasets.
import tensorflow as tf
from keras.models import Sequential
from keras.layers import Dense
from keras.wrappers.scikit_learn import KerasRegressor
def reg_model():
# create model
model = Sequential()
# Add and input and dense layer with 12 nurons
model.add(Dense(12, input_dim=df.shape[1] - 1, activation='relu'))
# Add output layer
model.add(Dense(1, activation='relu'))
# Compile model
model.compile(loss=tf.keras.losses.mape, optimizer='adam')
return model
def classif_model():
# create model
model = Sequential()
# Add and input and dense layer with 12 nurons
model.add(Dense(12, input_dim=df.shape[1] - 1, activation='sigmoid'))
# Add output layer
model.add(Dense(1, activation='sigmoid'))
# Compile model
model.compile(loss=tf.keras.losses.kld, optimizer='adam')
return model
Imputation Using k-NN:¶
The $k$ nearest neighbors is an algorithm that is used for simple classification. The algorithm uses ‘feature similarity’ to predict the values of any new data points. This means that the new point is assigned a value based on how closely it resembles the points in the training set. This can be very useful in making predictions about the missing values by finding the k’s closest neighbors to the observation with missing data and then imputing them based on the non-missing values in the neighborhood.
- How does it work?
It creates a basic mean impute then uses the resulting complete list to construct a KDTree. Then, it uses the resulting KDTree to compute nearest neighbours (NN). After it finds the k-NNs, it takes the weighted average of them.
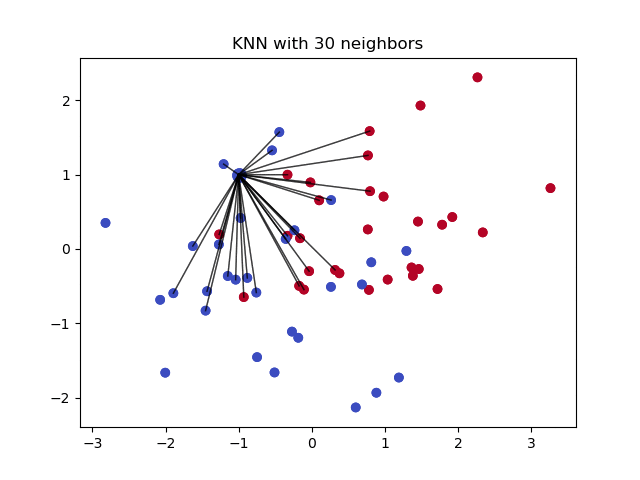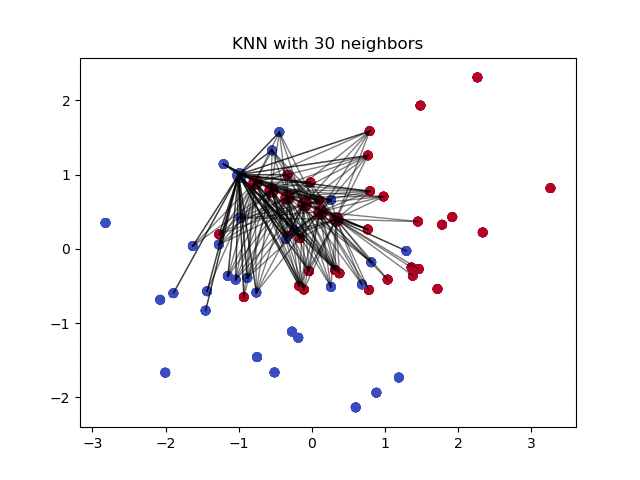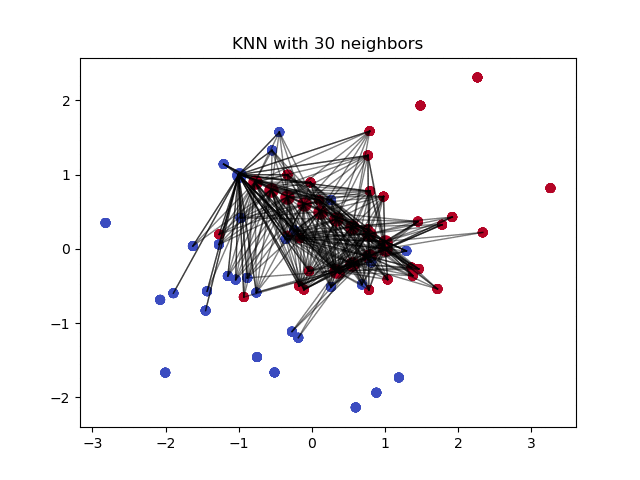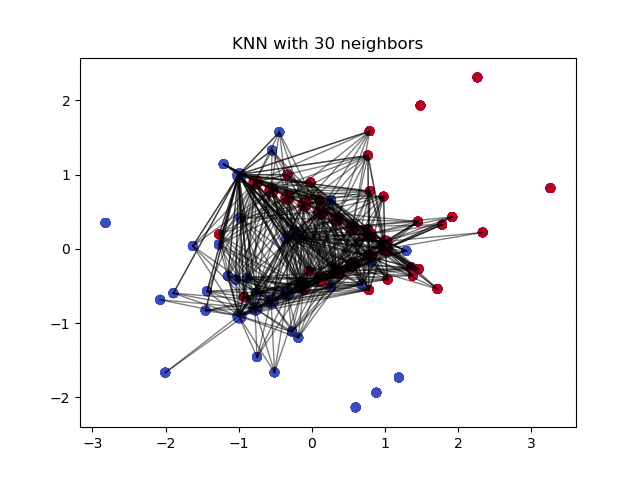
Pros:
- Can be much more accurate than the mean, median or most frequent imputation methods (It depends on the dataset).
Cons:
- Computationally expensive. KNN works by storing the whole training dataset in memory.
- K-NN is quite sensitive to outliers in the data (unlike SVM)
from sklearn.experimental import enable_iterative_imputer
from sklearn.impute import IterativeImputer
from sklearn.linear_model import BayesianRidge
from sklearn.neighbors import KNeighborsClassifier
reg_nn = KerasRegressor(build_fn=reg_model, epochs=20, batch_size=5, verbose=0)
classif_nn = KerasRegressor(build_fn=classif_model, epochs=20, batch_size=5, verbose=0)
reg = BayesianRidge()
knn = KNeighborsClassifier(n_neighbors=2)
z0 = np.round(IterativeImputer(estimator=reg,random_state=0).fit_transform(df.values))
z1 = IterativeImputer(estimator=knn, random_state=0).fit_transform(df.values)
z2 = np.round(IterativeImputer(estimator=reg_nn,random_state=0).fit_transform(df.values))
z3 = np.round(IterativeImputer(estimator=classif_nn,random_state=0).fit_transform(df.values))
df_imp0 = pd.DataFrame(z0, columns=df.columns)
df_imp1 = pd.DataFrame(z1, columns=df.columns)
df_imp2 = pd.DataFrame(z2, columns=df.columns)
df_imp3 = pd.DataFrame(z3, columns=df.columns)
print('\nMissing:')
print('\n',df)
print('\nBayesianRidgeRegressor:')
print('\n',df_imp0)
print('\nKNeighborsClassifier:')
print('\n',df_imp1)
print('\nNNRegressor:')
print('\n',df_imp2)
print('\nNNClassifier:')
print('\n',df_imp3)
Filling Missing Values With Model Advantages and Disadvantages¶
Advantages
- Could yield great results
- Should preserve variance
- Works with MAR and MNAR
Disavantages
- Can be computationally expensive
- Can take some time
Imputation Using Multivariate Imputation by Chained Equation (MICE)¶
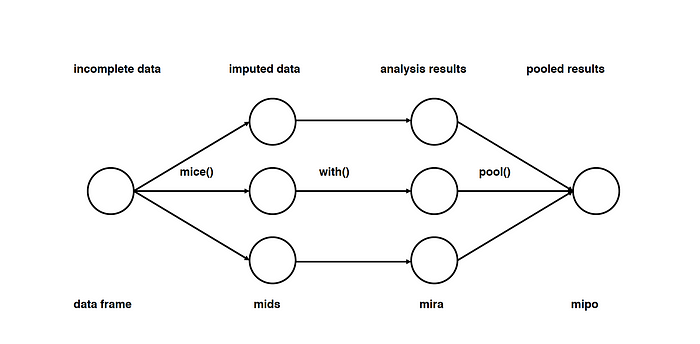
This type of imputation works by filling the missing data multiple times. Multiple Imputations (MIs) are much better than a single imputation as it measures the uncertainty of the missing values in a better way. The chained equations approach is also very flexible and can handle different variables of different data types (ie., continuous or binary) as well as complexities such as bounds or survey skip patterns.
from impyute.imputation.cs import mice
imputed_training = np.round(mice(df.astype(float).values))
print('\nMissing:')
print('\n',df)
print('\nNNRegressor:')
print('\n',df_imp2)
print('\nNNClassifier:')
print('\n',df_imp3)
print('\nMICE:')
print('\n',pd.DataFrame(imputed_training, columns=df.columns))