Probability & Hacker Statistics in python¶
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline
import seaborn as sns
sns.set(style="whitegrid", color_codes=True)
Parametric statistics¶
Parametric statistics is a branch of statistics which assumes that sample data come from a population that can be adequately modeled by a probability distribution that has a fixed set of parameters. Conversely a non-parametric model differs precisely in that the parameter set (or feature set in machine learning) is not fixed and can increase, or even decrease, if new relevant information is collected.
Nonparametric statistics¶
Nonparametric statistics is the branch of statistics that is not based solely on parametrized families of probability distributions (common examples of parameters are the mean and variance). Nonparametric statistics is based on either being distribution-free or having a specified distribution but with the distribution's parameters unspecified. Nonparametric statistics includes both descriptive statistics and statistical inference.
Descriptive Statistics¶
Descriptive statistics summarizes the data and are broken down into measures of central tendency (mean, median, and mode) and measures of variability (standard deviation, minimum/maximum values, range, kurtosis, and skewness).
Measures of central tendency¶
Meanis the average value of the data.Medianis the middle number of the data.Modeis the number that occurs most in the data.
Measures of variability¶
Standard deviationtells how much deviation is present in the data, i.e. how spread out the numbers are from the mean value.Minimum valuesmallest number in the data.Maximum valuelargest number in the data.Rangelargest number – smallest number.Kurtosisis a measure of tailedness. This number is related to the tails of the distribution. Higher kurtosis corresponds to more frequent extreme deviations (or outliers).Skewis a measure of symmetry.
Probability¶
- Probability is the measure of the likelihood that an event will occur. Representing the sample data distribution and probability being the area under the curve
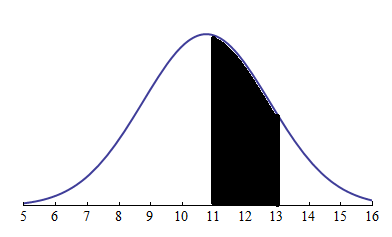
Likelihood¶
- Likelihood is a function of parameters within the parameter space that describes the probability of obtaining the observed data. Likelihood being the point on the curve
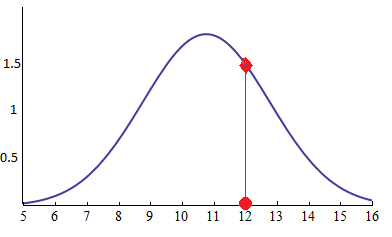
Discrete Random Variables¶
- A probability distribution is a table of values showing the probabilities of various outcomes of an experiment.
- A discrete variable is a variable which can only take a countable number of values. In this example, the number of heads can only take
4values(0, 1, 2, 3)and so the variable isdiscrete. The variable is said to be random if the sum of the probabilities is one.
Univariate¶
In mathematics, univariate refers to an expression, equation, function or polynomial of only one variable. Objects of any of these types involving more than one variable may be called multivariate.
Probability Mass Function¶
In probability and statistics, a probability mass function (PMF) is a function that gives the probability that a discrete random variable is exactly equal to some value. The probability mass function is often the primary means of defining a discrete probability distribution, and such functions exist for either scalar or multivariate random variables whose domain is discrete.
A probability mass function differs from a probability density function (PDF) in that the latter is associated with continuous rather than discrete random variables; the values of the probability density function are not probabilities as such: a PDF must be integrated over an interval to yield a probability.  The probability mass function
The probability mass function (pmf) p(S) specifies the probability distribution for the sum S of counts from two dice. For example, the figure shows that p(11) = 2/36 = 1/18. The pmf allows the computation of probabilities of events such as P(S > 9) = 1/12 + 1/18 + 1/36 = 1/6, and all other probabilities in the distribution.
Continuous Random Variables¶
A continuous random variable is a random variable where the data can take infinitely many values. For example, a random variable measuring the time taken for something to be done is continuous since there are an infinite number of possible times that can be taken.
Probability density function¶
In probability theory, a probability density function (PDF), or density of a continuous random variable, is a function whose value at any given sample (or point) in the sample space (the set of possible values taken by the random variable) can be interpreted as providing a relative likelihood that the value of the random variable would equal that sample. In other words, while the absolute likelihood for a continuous random variable to take on any particular value is 0 (since there are an infinite set of possible values to begin with), the value of the PDF at two different samples can be used to infer, in any particular draw of the random variable, how much more likely it is that the random variable would equal one sample compared to the other sample.
In a more precise sense, the PDF is used to specify the probability of the random variable falling within a particular range of values, as opposed to taking on any one value. This probability is given by the integral of this variable's PDF over that range—that is, it is given by the area under the density function but above the horizontal axis and between the lowest and greatest values of the range. The probability density function is nonnegative everywhere, and its integral over the entire space is equal to 1.  Boxplot and probability density function of a normal distribution
\begin{equation*}
N(0,σ^2).
\end{equation*}
Boxplot and probability density function of a normal distribution
\begin{equation*}
N(0,σ^2).
\end{equation*}
Variance¶
In probability theory and statistics, variance is the expectation of the squared deviation of a random variable from its mean. Informally, it measures how far a set of (random) numbers are spread out from their average value.  Example of samples from two populations with the same mean but different variances. The red population has mean
Example of samples from two populations with the same mean but different variances. The red population has mean 100 and variance 100 (SD=10) while the blue population has mean 100 and variance 2500 (SD=50).
Standard deviation¶
In statistics, the standard deviation (SD, also represented by the lower case Greek letter sigma σ for the population standard deviation or the Latin letter s for the sample standard deviation) is a measure of the amount of variation or dispersion of a set of values. A low standard deviation indicates that the values tend to be close to the mean (also called the expected value) of the set, while a high standard deviation indicates that the values are spread out over a wider range.  A plot of normal distribution (or bell-shaped curve) where each band has a width of 1 standard deviation
A plot of normal distribution (or bell-shaped curve) where each band has a width of 1 standard deviation
Covariance¶
In probability theory and statistics, covariance is a measure of the joint variability of two random variables. If the greater values of one variable mainly correspond with the greater values of the other variable, and the same holds for the lesser values, (i.e., the variables tend to show similar behavior), the covariance is positive. In the opposite case, when the greater values of one variable mainly correspond to the lesser values of the other, (i.e., the variables tend to show opposite behavior), the covariance is negative. The sign of the covariance therefore shows the tendency in the linear relationship between the variables. The magnitude of the covariance is not easy to interpret because it is not normalized and hence depends on the magnitudes of the variables. The normalized version of the covariance, the correlation coefficient, however, shows by its magnitude the strength of the linear relation.
Pearson correlation coefficient¶
In statistics, the Pearson correlation coefficient, also referred to as Pearson's r, the Pearson product-moment correlation coefficient (PPMCC) or the bivariate correlation, is a measure of the linear correlation between two variables X and Y. According to the Cauchy–Schwarz inequality it has a value between +1 and −1, where 1 is total positive linear correlation, 0 is no linear correlation, and −1 is total negative linear correlation. It is widely used in the sciences.  Several sets of
Several sets of (x, y) points, with the correlation coefficient of x and yfor each set. Note that the correlation reflects the non-linearity and direction of a linear relationship (top row), but not the slope of that relationship (middle), nor many aspects of nonlinear relationships (bottom). The figure in the center has a slope of 0 but in that case the correlation coefficient is undefined because the variance of Y is zero.
The np.random module and Bernoulli trials¶
You can think of a Bernoulli trial as a flip of a possibly biased coin. Specifically, each coin flip has a probability p of landing heads (success) and probability 1 − p of landing tails (failure). In this exercise, you will write a function to perform n Bernoulli trials, perform_bernoulli_trials(n, p), which returns the number of successes out of n Bernoulli trials, each of which has probability p of success. To perform each Bernoulli trial, use the np.random.random() function, which returns a random number between zero and one.
def perform_bernoulli_trials(n, p):
"""Perform n Bernoulli trials with success probability p
and return number of successes."""
# Initialize number of successes: n_success
n_success = 0
# Perform trials
for i in range(n):
# Choose random number between zero and one: random_number
random_number = np.random.random()
# If less than p, it's a success so add one to n_success
if random_number < p:
n_success += 1
return n_success
How many defaults might we expect?¶
Let's say a bank made 100 mortgage loans. It is possible that anywhere between 0 and 100 of the loans will be defaulted upon. You would like to know the probability of getting a given number of defaults, given that the probability of a default is p = 0.05. To investigate this, you will do a simulation. You will perform 100 Bernoulli trials using the perform_bernoulli_trials() and record how many defaults we get. Here, a success is a default. (Remember that the word "success" just means that the Bernoulli trial evaluates to True, i.e., did the loan recipient default?) You will do this for another 100 Bernoulli trials. And again and again until we have tried it 1000 times. Then, you will plot a histogram describing the probability of the number of defaults.
# Seed random number generator
np.random.seed(42)
# Initialize the number of defaults: n_defaults
n_defaults = np.empty(1000)
# Compute the number of defaults
for i in range(1000):
n_defaults[i] = perform_bernoulli_trials(100,0.05)
# Plot the histogram with default number of bins; label your axes
plt.figure(figsize=(12,6))
_ = plt.hist(n_defaults, density=True)
_ = plt.xlabel('number of defaults out of 100 loans')
_ = plt.ylabel('probability')
# Show the plot
plt.show()
Empirical Cumulative Distribution Function¶
What is an Empirical Cumulative Distribution Function?¶
An empirical cumulative distribution function (CDF) is a non-parametric estimator of the underlying CDF of a random variable. It assigns a probability of 1/n to each datum, orders the data from smallest to largest in value, and calculates the sum of the assigned probabilities up to and including each datum. The result is a step function that increases by 1/n at each datum.
def ecdf(data):
"""Compute ECDF for a one-dimensional array of measurements."""
# Number of data points: n
n = len(data)
# x-data for the ECDF: x
x = np.sort(data)
# y-data for the ECDF: y
y = np.arange(1, n+1) / n
return x, y
Will the bank fail?¶
Plot the number of defaults in your namespace as n_defaults, as a CDF. The ecdf() function above.
If interest rates are such that the bank will lose money if 10 or more of its loans are defaulted upon, what is the probability that the bank will lose money?
# Compute ECDF: x, y
x,y = ecdf(n_defaults)
# Plot the ECDF with labeled axes
plt.figure(figsize=(12,6))
_ = plt.plot(x,y, marker='.', linestyle='none', alpha=0.3)
_ = plt.xlabel('Defaults')
_ = plt.ylabel('Percentiles')
# Show the plot
plt.show()
# Compute the number of 100-loan simulations with 10 or more defaults: n_lose_money
n_lose_money = np.sum(n_defaults >= 10)
# Compute and print probability of losing money
print('Probability of losing money =', n_lose_money / len(n_defaults))
Sampling out of the Binomial distribution¶
Compute the probability mass function for the number of defaults we would expect for 100 loans. We will take 10,000 samples.
# Take 10,000 samples out of the binomial distribution: n_defaults
n_defaults = np.random.binomial(n = 100, p = 0.05, size=10000)
# Compute CDF: x, y
x,y = ecdf(n_defaults)
# Plot the CDF with axis labels
plt.figure(figsize=(12,6))
_ = plt.plot(x,y, marker='.', linestyle='none', alpha=0.3)
_ = plt.xlabel('Defaults')
_ = plt.ylabel('CDF')
# Show the plot
plt.show()
Plotting the Binomial PMF¶
We will plot the PMF of the Binomial distribution as a histogram. The trick is setting up the edges of the bins to pass to plt.hist() via the bins keyword argument. We want the bins centered on the integers. So, the edges of the bins should be -0.5, 0.5, 1.5, 2.5, ... up to max(n_defaults) + 1.5. You can generate an array like this using np.arange() and then subtracting 0.5 from the array.
# Compute bin edges: bins
bins = np.arange(0, max(n_defaults) + 1.5) - 0.5
# Generate histogram
plt.figure(figsize=(12,6))
plt.hist(n_defaults, density=True, bins=bins)
# Label axes
_ = plt.xlabel('Defaults')
_ = plt.ylabel('PMF')
# Show the plot
plt.show()
Poisson distribution¶
In probability theory and statistics, the Poisson distribution, named after French mathematician Siméon Denis Poisson, is a discrete probability distribution that expresses the probability of a given number of events occurring in a fixed interval of time or space if these events occur with a known constant rate and independently of the time since the last event. The Poisson distribution can also be used for the number of events in other specified intervals such as distance, area or volume.
For instance, an individual keeping track of the amount of mail they receive each day may notice that they receive an average number of 4 letters per day. If receiving any particular piece of mail does not affect the arrival times of future pieces of mail, i.e., if pieces of mail from a wide range of sources arrive independently of one another, then a reasonable assumption is that the number of pieces of mail received in a day obeys a Poisson distribution. Other examples that may follow a Poisson distribution include the number of phone calls received by a call center per hour.
Relationship between Binomial and Poisson distributions¶
You just heard that the Poisson distribution is a limit of the Binomial distribution for rare events. This makes sense if you think about the stories. Say we do a Bernoulli trial every minute for an hour, each with a success probability of 0.1. We would do 60 trials, and the number of successes is Binomially distributed, and we would expect to get about 6 successes. This is just like the Poisson story, where we get on average 6 hits on a website per hour. So, the Poisson distribution with arrival rate equal to np approximates a Binomial distribution for n Bernoulli trials with probability p of success (with n large and p small). Importantly, the Poisson distribution is often simpler to work with because it has only one parameter instead of two for the Binomial distribution.
Let's explore these two distributions computationally. You will compute the mean and standard deviation of samples from a Poisson distribution with an arrival rate of 10. Then, you will compute the mean and standard deviation of samples from a Binomial distribution with parameters n and p such that np = 10.
# Draw 10,000 samples out of Poisson distribution: samples_poisson
samples_poisson = np.random.poisson(10, 10000)
# Print the mean and standard deviation
print('Poisson: ', np.mean(samples_poisson),
np.std(samples_poisson))
# Specify values of n and p to consider for Binomial: n, p
n = [20, 100, 1000]
p = [0.5, 0.1, 0.01]
# Draw 10,000 samples for each n,p pair: samples_binomial
for i in range(3):
samples_binomial = np.random.binomial(1000, 0.01, 10000)
# Print results
print('n =', n[i], 'Binom:', np.mean(samples_binomial),
np.std(samples_binomial))
Was 2015 anomalous?¶
1990 and 2015 featured the most no-hitters of any season of baseball (there were seven). Given that there are on average 251/115 no-hitters per season, what is the probability of having seven or more in a season?
# Draw 10,000 samples out of Poisson distribution: n_nohitters
n_nohitters = np.random.poisson(251/115, 10000)
# Compute number of samples that are seven or greater: n_large
n_large = np.sum(n_nohitters >= 7)
# Compute probability of getting seven or more: p_large
p_large = n_large / len(n_nohitters)
# Print the result
print('Probability of seven or more no-hitters:', p_large)
Normal distribution¶
In probability theory, the normal (or Gaussian or Gauss or Laplace–Gauss) distribution is a very common continuous probability distribution. Normal distributions are important in statistics and are often used in the natural and social sciences to represent real-valued random variables whose distributions are not known. A random variable with a Gaussian distribution is said to be normally distributed and is called a normal deviate.
The normal distribution is useful because of the central limit theorem. In its most general form, under some conditions (which include finite variance), it states that averages of samples of observations of random variables independently drawn from the same distribution converge in distribution to the normal, that is, they become normally distributed when the number of observations is sufficiently large. Physical quantities that are expected to be the sum of many independent processes (such as measurement errors) often have distributions that are nearly normal. Moreover, many results and methods (such as propagation of uncertainty and least squares parameter fitting) can be derived analytically in explicit form when the relevant variables are normally distributed.
The Normal PDF¶
In this exercise, you will explore the Normal PDF and also learn a way to plot a PDF of a known distribution using hacker statistics. Specifically, you will plot a Normal PDF for various values of the variance.
# Draw 100000 samples from Normal distribution with stds of interest: samples_std1, samples_std3, samples_std10
samples_std1 = np.random.normal(20, 1, 100000)
samples_std3 = np.random.normal(20, 3, 100000)
samples_std10 = np.random.normal(20, 10, 100000)
# Make histograms
plt.figure(figsize=(12,6))
_ = plt.hist(samples_std1, bins=100, density=True, histtype='step')
_ = plt.hist(samples_std3, bins=100, density=True, histtype='step')
_ = plt.hist(samples_std10, bins=100, density=True, histtype='step')
# Make a legend, set limits and show plot
_ = plt.legend(('std = 1', 'std = 3', 'std = 10'))
plt.ylim(-0.01, 0.42)
plt.show()
The Normal CDF¶
Now that you have a feel for how the Normal PDF looks, let's consider its CDF.
# Generate CDFs
x_std1, y_std1 = ecdf(samples_std1)
x_std3, y_std3 = ecdf(samples_std3)
x_std10, y_std10 = ecdf(samples_std10)
# Plot CDFs
plt.figure(figsize=(12,6))
_ = plt.plot(x_std1,y_std1, marker='.', linestyle='none', alpha=0.3)
_ = plt.plot(x_std3,y_std3, marker='.', linestyle='none', alpha=0.3)
_ = plt.plot(x_std10,y_std10, marker='.', linestyle='none', alpha=0.3)
# Make a legend and show the plot
_ = plt.legend(('std = 1', 'std = 3', 'std = 10'), loc='lower right')
plt.show()
Are the returns Normally distributed?¶
import pandas as pd
import pandas_datareader.data as web
start = pd.datetime(2010, 1, 1)
end = pd.datetime(2019,11,14)
spy = web.DataReader("SPY", "yahoo", start, end)
rets = spy.Close.pct_change().fillna(0.0)
# Compute mean and standard deviation: mu, sigma
mu = rets.mean()
sigma = rets.std()
# Sample out of a normal distribution with this mu and sigma: samples
samples = np.random.normal(mu, sigma, 10000)
# Get the CDF of the samples and of the data
x_theor, y_theor = ecdf(samples)
x, y = ecdf(rets)
# Plot the CDFs and show the plot
plt.figure(figsize=(12,6))
_ = plt.plot(x_theor, y_theor, label='Normal')
_ = plt.plot(x, y, marker='.', linestyle='none', label='Returns')
_ = plt.xlabel('SPY Returns')
_ = plt.ylabel('CDF')
_ = plt.legend()
plt.show()
- What are the chances of an up day? Assume that the returns are Normally distributed, what is the probability that SPY has a return greater then 1%?
# Take a million samples out of the Normal distribution: samples
samples = np.random.normal(mu,sigma,1000000)
# Compute the fraction that are faster than 144 seconds: prob
prob = np.sum(samples>=0.01) / len(samples)
# Print the result
print('Probability of returns >= 1% during the sample period:', round(prob,2))
If you have a story, you can simulate it!¶
Sometimes, the story describing our probability distribution does not have a named distribution to go along with it. In these cases, fear not! You can always simulate it.
A Hitting the cycle is a rare baseball event. When a batter hits the cycle, he gets all four kinds of hits, a single, double, triple, and home run, in a single game. This can be modeled as a Poisson process, so the time between hits of the cycle are also Exponentially distributed.
How long must we wait to see both a no-hitter and then a batter hit the cycle? The idea is that we have to wait some time for the no-hitter, and then after the no-hitter, we have to wait for hitting the cycle. Stated another way, what is the total waiting time for the arrival of two different Poisson processes? The total waiting time is the time waited for the no-hitter, plus the time waited for the hitting the cycle.
A function to sample out of the distribution described by this story.
def successive_poisson(tau1, tau2, size=1):
"""Compute time for arrival of 2 successive Poisson processes."""
# Draw samples out of first exponential distribution: t1
t1 = np.random.exponential(size, tau1)
# Draw samples out of second exponential distribution: t2
t2 = np.random.exponential(size, tau2)
waiting_times = t1 + t2
plt.figure(figsize=(12,6))
plt.hist(waiting_times, density=True, bins=100, histtype='step')
# Label axes
_ = plt.xlabel('waiting_times')
_ = plt.ylabel('PDF')
# Show the plot
plt.show()
Distribution of no-hitters and cycles¶
Now, you'll use your sampling function to compute the waiting time to observe a no-hitter and hitting of the cycle. The mean waiting time for a no-hitter is 764 games, and the mean waiting time for hitting the cycle is 715 games.
_ = successive_poisson(715, 715, size=100000)
no_hitters = pd.read_csv('mlb_nohitters.csv')
no_hitters.info()
no_hitters.tail()
nohitter_times = no_hitters.game_number
How often do we get no-hitters?¶
The number of games played between each no-hitter in the modern era (1901-2015) of Major League Baseball is stored in the array nohitter_times.
If you assume that no-hitters are described as a Poisson process, then the time between no-hitters is Exponentially distributed. As you have seen, the Exponential distribution has a single parameter, which we will call τ, the typical interval time. The value of the parameter τ that makes the exponential distribution best match the data is the mean interval time (where time is in units of number of games) between no-hitters.
Compute the value of this parameter from the data. Then, use np.random.exponential() to "repeat" the history of Major League Baseball by drawing inter-no-hitter times from an exponential distribution with the τ you found and plot the histogram as an approximation to the PDF.
# Seed random number generator
np.random.seed(42)
# Compute mean no-hitter time: tau
tau = nohitter_times.mean()
# Draw out of an exponential distribution with parameter tau: inter_nohitter_time
inter_nohitter_time = np.random.exponential(tau, 100000)
# Plot the PDF and label axes
plt.figure(figsize=(12,6))
_ = plt.hist(inter_nohitter_time,
bins=50, density=True, histtype='step')
_ = plt.xlabel('Games between no-hitters')
_ = plt.ylabel('PDF')
# Show the plot
plt.show()
Do the data follow our story?¶
You have modeled no-hitters using an Exponential distribution. Create an ECDF of the real data. Overlay the theoretical CDF with the ECDF from the data. This helps you to verify that the Exponential distribution describes the observed data.
# Create an ECDF from real data: x, y
x, y = ecdf(nohitter_times)
# Create a CDF from theoretical samples: x_theor, y_theor
x_theor, y_theor = ecdf(inter_nohitter_time)
# Overlay the plots
plt.figure(figsize=(12,6))
plt.plot(x_theor, y_theor)
plt.plot(x, y, marker= '.', linestyle='none')
# Margins and axis labels
plt.margins(0.02)
plt.xlabel('Games between no-hitters')
plt.ylabel('CDF')
# Show the plot
plt.show()
How is this parameter optimal?¶
Now sample out of an exponential distribution with τ being twice as large as the optimal τ. Do it again for τ half as large. Make CDFs of these samples and overlay them with your data. You can see that they do not reproduce the data as well. Thus, the τ you computed from the mean inter-no-hitter times is optimal in that it best reproduces the data.
# Plot the theoretical CDFs
plt.figure(figsize=(12,6))
plt.plot(x_theor, y_theor)
plt.plot(x, y, marker='.', linestyle='none')
plt.margins(0.02)
plt.xlabel('Games between no-hitters')
plt.ylabel('CDF')
# Take samples with half tau: samples_half
samples_half = np.random.exponential(tau/2, 10000)
# Take samples with double tau: samples_double
samples_double = np.random.exponential(2*tau, 10000)
# Generate CDFs from these samples
x_half, y_half = ecdf(samples_half)
x_double, y_double = ecdf(samples_double)
# Plot these CDFs as lines
_ = plt.plot(x_half, y_half)
_ = plt.plot(x_double, y_double)
# Show the plot
plt.show()
EDA of literacy/fertility data¶
In the next few exercises, we will look at the correlation between female literacy and fertility (defined as the average number of children born per woman) throughout the world. For ease of analysis and interpretation, we will work with the illiteracy rate.
It is always a good idea to do some EDA ahead of our analysis.
female_literacy_fertility = pd.read_csv('female_literacy_fertility.csv')
female_literacy_fertility.info()
female_literacy_fertility.tail()
fertility = np.array(female_literacy_fertility.fertility)
illiteracy = np.array(female_literacy_fertility['female literacy'])
Computing the Pearson correlation coefficient¶
The Pearson correlation coefficient, also called the Pearson r, is often easier to interpret than the covariance. It is computed using the np.corrcoef() function. Like np.cov(), it takes two arrays as arguments and returns a 2D array. Entries [0,0] and [1,1] are necessarily equal to 1.
def pearson_r(x, y):
"""Compute Pearson correlation coefficient between two arrays."""
# Compute correlation matrix: corr_mat
corr_mat = np.corrcoef(x,y)
# Return entry [0,1]
return corr_mat[0,1]
EDA of literacy/fertility data¶
Plot the fertility versus illiteracy and compute the Pearson correlation coefficient.
# Plot the illiteracy rate versus fertility
plt.figure(figsize=(12,6))
_ = plt.plot(illiteracy, fertility, marker='.', linestyle='none')
# Set the margins and label axes
plt.margins(0.02)
_ = plt.ylabel('percent fertile')
_ = plt.xlabel('percent illiterate')
# Show the plot
plt.show()
# Show the Pearson correlation coefficient
print(pearson_r(illiteracy, fertility))
Linear regression¶
We will assume that fertility is a linear function of the female illiteracy rate. That is, f = ai + b, where a is the slope and b is the intercept. We can think of the intercept as the minimal fertility rate, probably somewhere between one and two. The slope tells us how the fertility rate varies with illiteracy. We can find the best fit line using np.polyfit().
# Plot the illiteracy rate versus fertility
plt.figure(figsize=(12,6))
_ = plt.plot(illiteracy, fertility, marker='.', linestyle='none')
plt.margins(0.02)
_ = plt.xlabel('percent illiterate')
_ = plt.ylabel('fertility')
# Perform a linear regression using np.polyfit(): a, b
a, b = np.polyfit(illiteracy,fertility,1)
# Print the results to the screen
print('slope =', a, 'children per woman / percent illiterate')
print('intercept =', b, 'children per woman')
# Make theoretical line to plot
x = np.array([0, 100])
y = a * x + b
# Add regression line to your plot
_ = plt.plot(x, y)
# Draw the plot
plt.show()
How is it optimal?¶
The function np.polyfit() that you used to get your regression parameters finds the optimal slope and intercept. It is optimizing the sum of the squares of the residuals, also known as RSS (for residual sum of squares). Plot the function that is being optimized, the RSS, versus the slope parameter a. To do this, fix the intercept to be what you found in the optimization. Then, plot the RSS vs. the slope.
# Specify slopes to consider: a_vals
a_vals = np.linspace(0, 0.1, 200)
# Initialize sum of square of residuals: rss
rss = np.empty_like(a_vals)
# Compute sum of square of residuals for each value of a_vals
for i, a in enumerate(a_vals):
rss[i] = np.sum((fertility - a*illiteracy - b)**2)
# Plot the RSS
plt.figure(figsize=(12,6))
plt.plot(a_vals, rss, '-')
plt.xlabel('slope (children per woman / percent illiterate)')
plt.ylabel('sum of square of residuals')
plt.show()
Linear regression on appropriate Anscombe data¶
For practice, perform a linear regression on the data set from Anscombe's quartet that is most reasonably interpreted with linear regression.
anscombe = pd.read_csv('anscombe.csv')
anscombe = anscombe[1:].astype(float)
anscombe.columns = ['x1','y1','x2','y2','x3','y3','x4','y4']
anscombe.info()
anscombe.tail()
x = np.array(anscombe['x1'])
y = np.array(anscombe['y1'])
# Perform linear regression: a, b
a, b = np.polyfit(x,y,1)
# Print the slope and intercept
print(a, b)
# Generate theoretical x and y data: x_theor, y_theor
x_theor = np.array([3, 15])
y_theor = a * x_theor + b
# Plot the Anscombe data and theoretical line
plt.figure(figsize=(12,6))
_ = plt.plot(x, y, marker='.', linestyle='none')
_ = plt.plot(x_theor, y_theor)
# Label the axes
plt.xlabel('x')
plt.ylabel('y')
# Show the plot
plt.show()
Linear regression on all Anscombe data¶
Now, to verify that all four of the Anscombe data sets have the same slope and intercept from a linear regression, you will compute the slope and intercept for each set. The data are stored in lists; anscombe_x = [x1, x2, x3, x4] and anscombe_y = [y1, y2, y3, y4], where, for example, x2 and y2 are the x and y values for the second Anscombe data set.
x1 = np.array(anscombe['x1'])
y1 = np.array(anscombe['y1'])
x2 = np.array(anscombe['x2'])
y2 = np.array(anscombe['y2'])
x3 = np.array(anscombe['x3'])
y3 = np.array(anscombe['y3'])
x4 = np.array(anscombe['x4'])
y4 = np.array(anscombe['y4'])
anscombe_x = [x1, x2, x3, x4]
anscombe_y = [y1, y2, y3, y4]
# Iterate through x,y pairs
for x, y in zip(anscombe_x, anscombe_y):
# Compute the slope and intercept: a, b
a, b = np.polyfit(x,y,1)
# Print the result
print('slope:', a, 'intercept:', b)
# Iterate through x,y pairs
for x, y in zip(anscombe_x, anscombe_y):
# Compute the slope and intercept: a, b
plt.figure(figsize=(12,6))
_ = plt.scatter(x, y, marker='.', alpha=0.75, s=500)
# Label the axes
plt.xlabel('x')
plt.ylabel('y')
# Show the plot
plt.show()
Sampling With/Without Replacement¶
Suppose we have a bowl of 100 unique numbers from 0 to 99. We want to select a random sample of numbers from the bowl. After we pick a number from the bowl, we can put the number aside or we can put it back into the bowl. If we put the number back in the bowl, it may be selected more than once; if we put it aside, it can selected only one time.
- When a population element can be selected more than one time, we are sampling
with replacement. - When a population element can be selected only one time, we are sampling
without replacement.
Bootstrap Method¶
The basic idea of bootstrap is make inference about a estimate(such as sample mean) for a population parameter θ (such as population mean) on sample data. It is a resampling method by independently sampling with replacement from an existing sample data with same sample size n, and performing inference among these resampled data.
Generally, bootstrap involves the following steps: 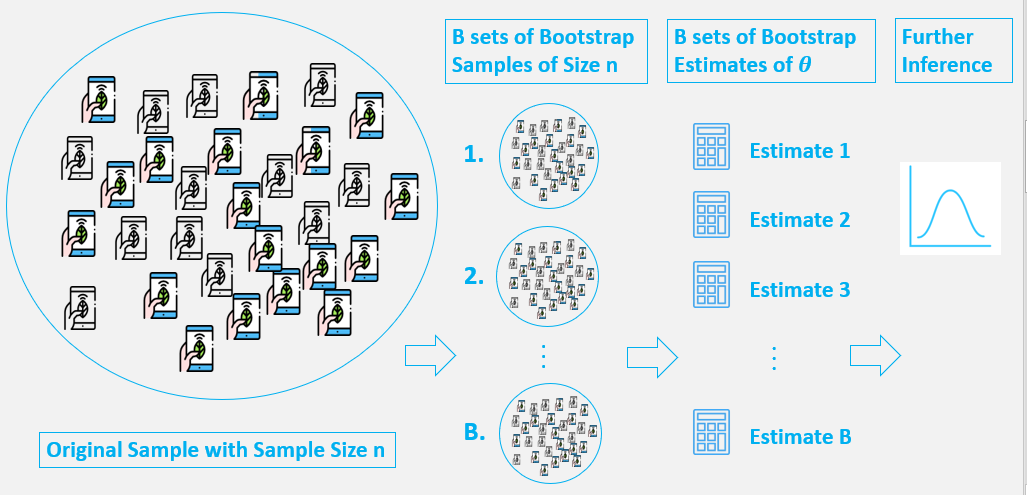
- A sample from population with sample size
n. - Draw a sample from the original sample data
with replacementwith size n, and replicate B times, each re-sampled sample is called a Bootstrap Sample, and there will totally B Bootstrap Samples. - Evaluate the
statisticofθfor each Bootstrap Sample, and there will be totally B estimates ofθ. - Construct a
sampling distributionwith these B Bootstrap statistics and use it to make further statistical inference, such as:
- Estimating the standard error of statistic for
θ. - Obtaining a Confidence Interval for
θ.
We can see we generate new data points by re-sampling from an existing sample, and make inference just based on these new data points.
df = pd.read_fwf('sheffield_weather_station.csv', skiprows=8)
print(df.shape)
df.head()
rainfall = df.rain
Visualizing bootstrap samples¶
Generate bootstrap samples from the set of annual rainfall data measured at the Sheffield Weather Station in the UK from 1883 to 2015. The data are stored in the NumPy array rainfall in units of millimeters (mm). By graphically displaying the bootstrap samples with an ECDF, you can get a feel for how bootstrap sampling allows probabilistic descriptions of data.
for _ in range(1000):
# Generate bootstrap sample: bs_sample
bs_sample = np.random.choice(rainfall, size=len(rainfall))
# Compute and plot ECDF from bootstrap sample
x, y = ecdf(bs_sample)
_ = plt.plot(x, y, marker='.', linestyle='none',
color='blue', alpha=0.1)
# Compute and plot ECDF from original data
x, y = ecdf(rainfall)
_ = plt.plot(x, y, marker='.', alpha=0.1, color='red')
# Make margins and label axes
plt.margins(0.02)
_ = plt.xlabel('yearly rainfall (mm)')
_ = plt.ylabel('ECDF')
# Show the plot
plt.show()
Generating many bootstrap replicates¶
Now you'll write another function, draw_bs_reps(data, func, size=1), which generates many bootstrap replicates from the data set. This function will come in handy for you again and again as you compute confidence intervals and later when you do hypothesis tests.
def bootstrap_replicate_1d(data, func):
return func(np.random.choice(data, size=len(data)))
def draw_bs_reps(data, func, size=1):
"""Draw bootstrap replicates."""
# Initialize array of replicates: bs_replicates
bs_replicates = np.empty(size)
# Generate replicates
for i in range(size):
bs_replicates[i] = bootstrap_replicate_1d(data, func)
return bs_replicates
Bootstrap replicates of the mean and the SEM¶
In this exercise, you will compute a bootstrap estimate of the probability density function of the mean annual rainfall at the Sheffield Weather Station. Remember, we are estimating the mean annual rainfall we would get if the Sheffield Weather Station could repeat all of the measurements from 1883 to 2015 over and over again. This is a probabilistic estimate of the mean. You will plot the PDF as a histogram, and you will see that it is Normal.
In fact, it can be shown theoretically that under not-too-restrictive conditions, the value of the mean will always be Normally distributed. (This does not hold in general, just for the mean and a few other statistics.) The standard deviation of this distribution, called the standard error of the mean, or SEM, is given by the standard deviation of the data divided by the square root of the number of data points. I.e., for a data set, sem = np.std(data) / np.sqrt(len(data)). Using hacker statistics, you get this same result without the need to derive it, but you will verify this result from your bootstrap replicates.
# Take 10,000 bootstrap replicates of the mean: bs_replicates
bs_replicates = draw_bs_reps(rainfall, np.mean, size=10000)
# Compute and print SEM
sem = np.std(rainfall) / np.sqrt(len(rainfall))
print(sem)
# Compute and print standard deviation of bootstrap replicates
bs_std = print(np.std(bs_replicates))
print(bs_std)
# Make a histogram of the results
plt.figure(figsize=(12,6))
_ = plt.hist(bs_replicates, bins=50, density=True)
_ = plt.xlabel('mean annual rainfall (mm)')
_ = plt.ylabel('PDF')
# Show the plot
plt.show()
Confidence intervals of rainfall data¶
A confidence interval gives upper and lower bounds on the range of parameter values you might expect to get if we repeat our measurements. For named distributions, you can compute them analytically or look them up, but one of the many beautiful properties of the bootstrap method is that you can take percentiles of your bootstrap replicates to get your confidence interval. Conveniently, you can use the np.percentile() function.
conf_int = np.percentile(bs_replicates, [2.5,97.5])
conf_int
Plot rainfall data bootstrapped samples mean and standard deviation as well as there 95% confidence intervals
import seaborn as sns
# construct the simulated sampling distribution
sample_props = []
sample_props0 = []
for _ in range(1000):
sample = np.random.choice(rainfall, size=len(rainfall))
sample_props.append(sample.mean())
sample_props0.append(sample.std())
# Plot the simulated sampling distribution
sns.distplot(sample_props, bins=50)
# Compute the 95% confidence interval: conf_int
conf_int = np.percentile(sample_props, [2.5,97.5])
# Plot the confidence intervals
plt.axvline(conf_int[0], color='red', linestyle='dashed')
plt.axvline(conf_int[1], color='red', linestyle='dashed')
plt.title('mean')
plt.show()
print('\nMean confidence interval',conf_int)
sns.distplot(sample_props0, bins=50)
# Compute the 95% confidence interval: conf_int
conf_int0 = np.percentile(sample_props0, [2.5,97.5])
# Plot the confidence intervals
plt.axvline(conf_int0[0], color='red', linestyle='dashed')
plt.axvline(conf_int0[1], color='red', linestyle='dashed')
plt.title('std')
plt.show()
print('\nStandard deviation confidence interval',conf_int0)
Bootstrap replicates of other statistics¶
We saw in a previous exercise that the mean is Normally distributed. This does not necessarily hold for other statistics, but no worry: as hackers, we can always take bootstrap replicates! In this exercise, you'll generate bootstrap replicates for the variance of the annual rainfall at the Sheffield Weather Station and plot the histogram of the replicates.
# Generate 10,000 bootstrap replicates of the variance: bs_replicates
bs_replicates = draw_bs_reps(rainfall, np.var, size=10000)
# Put the variance in units of square centimeters
bs_replicates = bs_replicates / 100
# Make a histogram of the results
plt.figure(figsize=(12,6))
_ = plt.hist(bs_replicates, density=True, bins=50)
_ = plt.xlabel('variance of annual rainfall (sq. cm)')
_ = plt.ylabel('PDF')
# Show the plot
plt.show()
Confidence interval on the rate of no-hitters¶
Consider again the inter-no-hitter intervals for the modern era of baseball. Generate 10,000 bootstrap replicates of the optimal parameter τ. Plot a histogram of your replicates and report a 95% confidence interval.
# Draw bootstrap replicates of the mean no-hitter time (equal to tau): bs_replicates
bs_replicates = draw_bs_reps(nohitter_times, np.mean, size=10000)
# Compute the 95% confidence interval: conf_int
conf_int = np.percentile(bs_replicates, [2.5,97.5])
# Print the confidence interval
print('95% confidence interval =', conf_int, 'games')
# Plot the histogram of the replicates
plt.figure(figsize=(12,6))
_ = plt.hist(bs_replicates, bins=50, density=True)
_ = plt.xlabel(r'$\tau$ (games)')
_ = plt.ylabel('PDF')
# Show the plot
plt.show()
A function to do pairs bootstrap¶
Pairs bootstrap involves resampling pairs of data. Each collection of pairs fit with a line, in this case using np.polyfit(). We do this again and again, getting bootstrap replicates of the parameter values. To have a useful tool for doing pairs bootstrap, you will write a function to perform pairs bootstrap on a set of x,y data.
def draw_bs_pairs_linreg(x, y, size=1):
"""Perform pairs bootstrap for linear regression."""
# Set up array of indices to sample from: inds
inds = np.arange(len(x))
# Initialize replicates: bs_slope_reps, bs_intercept_reps
bs_slope_reps = np.empty(size)
bs_intercept_reps = np.empty(size)
# Generate replicates
for i in range(size):
bs_inds = np.random.choice(inds, size=len(inds))
bs_x, bs_y = x[bs_inds], y[bs_inds]
bs_slope_reps[i], bs_intercept_reps[i] = np.polyfit(bs_x,bs_y,1)
return bs_slope_reps, bs_intercept_reps
Pairs bootstrap of literacy/fertility data¶
Using the function you just wrote, perform pairs bootstrap to plot a histogram describing the estimate of the slope from the illiteracy/fertility data. Also report the 95% confidence interval of the slope. The data is available to you in the NumPy arrays illiteracy and fertility.
# Generate replicates of slope and intercept using pairs bootstrap
bs_slope_reps, bs_intercept_reps = draw_bs_pairs_linreg(illiteracy, fertility, size=1000)
# Compute and print 95% CI for slope
print(np.percentile(bs_slope_reps, [2.5,97.5]))
# Plot the histogram
plt.figure(figsize=(12,6))
_ = plt.hist(bs_slope_reps, bins=50, density=True)
_ = plt.xlabel('slope')
_ = plt.ylabel('PDF')
plt.show()
Plotting bootstrap regressions¶
A nice way to visualize the variability we might expect in a linear regression is to plot the line you would get from each bootstrap replicate of the slope and intercept. Do this for the first 100 of your bootstrap replicates of the slope and intercept.
# Generate array of x-values for bootstrap lines: x
x = np.array([0, 100])
# Plot the bootstrap lines
for i in range(100):
_ = plt.plot(x, bs_slope_reps[i]*x + bs_intercept_reps[i],
linewidth=0.5, alpha=0.2, color='red')
# Plot the data
_ = plt.plot(illiteracy, fertility, marker='.', linestyle='none')
# Label axes, set the margins, and show the plot
_ = plt.xlabel('illiteracy')
_ = plt.ylabel('fertility')
plt.margins(0.02)
plt.show()
Permutation:¶
Random reordering or entries in an array.
Generating a permutation sample¶
Permutation sampling is a great way to simulate the hypothesis that two variables have identical probability distributions. This is often a hypothesis you want to test, so in this exercise, you will write a function to generate a permutation sample from two data sets.
Remember, a permutation sample of two arrays having respectively n1 and n2 entries is constructed by concatenating the arrays together, scrambling the contents of the concatenated array, and then taking the first n1 entries as the permutation sample of the first array and the last n2 entries as the permutation sample of the second array.
def permutation_sample(data1, data2):
"""Generate a permutation sample from two data sets."""
# Concatenate the data sets: data
data = np.concatenate((data1, data2))
# Permute the concatenated array: permuted_data
permuted_data = np.random.permutation(data)
# Split the permuted array into two: perm_sample_1, perm_sample_2
perm_sample_1 = permuted_data[:len(data1)]
perm_sample_2 = permuted_data[len(data1):]
return perm_sample_1, perm_sample_2
Visualizing permutation sampling¶
To help see how permutation sampling works, in this exercise you will generate permutation samples and look at them graphically.
We will use the Sheffield Weather Station data again, this time considering the monthly rainfall in June (a dry month) and November (a wet month). We expect these might be differently distributed, so we will take permutation samples to see how their ECDFs would look if they were identically distributed.
rain_june, rain_november = df[df['mm']==6]['rain'], df[df['mm']==11]['rain']
for i in range(50):
# Generate permutation samples
perm_sample_1, perm_sample_2 = permutation_sample(rain_june,rain_november)
# Compute ECDFs
x_1, y_1 = ecdf(perm_sample_1)
x_2, y_2 = ecdf(perm_sample_2)
# Plot ECDFs of permutation sample
_ = plt.plot(x_1, y_1, marker='.', linestyle='none',
color='red', alpha=0.02)
_ = plt.plot(x_2, y_2, marker='.', linestyle='none',
color='blue', alpha=0.02)
# Create and plot ECDFs from original data
x_1, y_1 = ecdf(rain_june)
x_2, y_2 = ecdf(rain_november)
_ = plt.plot(x_1, y_1, marker='.', linestyle='none', color='red')
_ = plt.plot(x_2, y_2, marker='.', linestyle='none', color='blue')
# Label axes, set margin, and show plot
plt.margins(0.02)
_ = plt.xlabel('monthly rainfall (mm)')
_ = plt.ylabel('ECDF')
plt.show()
Null hypothesis¶
In inferential statistics, the null hypothesis is a general statement or default position that there is nothing new happening, like there is no association among groups, or no relationship between two measured phenomena. Testing (accepting or rejecting) the null hypothesis—and thus concluding that there are or are not grounds for believing that there is a relationship between two phenomena (e.g. that a potential treatment has a measurable effect)—is a central task in the modern practice of science; the field of statistics gives precise criteria for rejecting a null hypothesis.
The null hypothesis is generally assumed to be true until evidence indicates otherwise.
Test statistics¶
A test statistic is a statistic (a quantity derived from the sample) used in statistical hypothesis testing. A hypothesis test is typically specified in terms of a test statistic, considered as a numerical summary of a data-set that reduces the data to one value that can be used to perform the hypothesis test. In general, a test statistic is selected or defined in such a way as to quantify, within observed data, behaviours that would distinguish the null from the alternative hypothesis.
When performing hypothesis tests, your choice of test statistic should be be pertinent to the question you are seeking to answer in your hypothesis test.
What is a p-value?¶
The p-value is generally a measure of the probability of observing a test statistic equally or more extreme than the one you observed, given that the null hypothesis is true.
Generating permutation replicates¶
A permutation replicate is a single value of a statistic computed from a permutation sample. As the draw_bs_reps() function is useful for you to generate bootstrap replicates, it is useful to have a similar function, draw_perm_reps(), to generate permutation replicates.
def draw_perm_reps(data_1, data_2, func, size=1):
"""Generate multiple permutation replicates."""
# Initialize array of replicates: perm_replicates
perm_replicates = np.empty(size)
for i in range(size):
# Generate permutation sample
perm_sample_1, perm_sample_2 = permutation_sample(data_1, data_2)
# Compute the test statistic
perm_replicates[i] = func(perm_sample_1, perm_sample_2)
return perm_replicates
Look before you leap: EDA before hypothesis testing¶
Kleinteich and Gorb (Sci. Rep., 4, 5225, 2014) performed an interesting experiment with South American horned frogs. They held a plate connected to a force transducer, along with a bait fly, in front of them. They then measured the impact force and adhesive force of the frog's tongue when it struck the target.
Frog A is an adult and Frog B is a juvenile. The researchers measured the impact force of 20 strikes for each frog. In the next exercise, we will test the hypothesis that the two frogs have the same distribution of impact forces. But, remember, it is important to do EDA first! Let's make a bee swarm plot for the data. They are stored in a Pandas data frame, df, where column ID is the identity of the frog and column impact_force is the impact force in Newtons (N).
df_f = pd.read_excel('frog_tongue0.xlsx')
print(df_f.shape)
df_f.head()
# Make bee swarm plot
_ = sns.swarmplot(df_f['ID'], df_f['impact force / body weight'], data=df_f)
# Label axes
_ = plt.xlabel('frog')
_ = plt.ylabel('impact force (N)')
# Show the plot
plt.show()
Permutation test on frog data¶
The average strike force of Frog A was 0.71 Newtons (N), and that of Frog B was 0.42 N for a difference of 0.29 N. It is possible the frogs strike with the same force and this observed difference was by chance. You will compute the probability of getting at least a 0.29 N difference in mean strike force under the hypothesis that the distributions of strike forces for the two frogs are identical. We use a permutation test with a test statistic of the difference of means to test this hypothesis.
force_a, force_b = df_f[df_f['ID']=='I']['impact force / body weight'], df_f[df_f['ID']=='II']['impact force / body weight']
def diff_of_means(data_1, data_2):
"""Difference in means of two arrays."""
# The difference of means of data_1, data_2: diff
diff = np.mean(data_1) - np.mean(data_2)
return diff
# Compute difference of mean impact force from experiment: empirical_diff_means
empirical_diff_means = diff_of_means(force_a, force_b)
# Draw 10,000 permutation replicates: perm_replicates
perm_replicates = draw_perm_reps(force_a, force_b,
diff_of_means, size=10000)
# Compute p-value: p
p = np.sum(perm_replicates >= empirical_diff_means) / len(perm_replicates)
# Print the result
print('p-value =', p)
A one-sample bootstrap hypothesis test¶
Another juvenile frog was studied, Frog C, and you want to see if Frog B and Frog C have similar impact forces. Unfortunately, you do not have Frog C's impact forces available, but you know they have a mean of 0.55 N. Because you don't have the original data, you cannot do a permutation test, and you cannot assess the hypothesis that the forces from Frog B and Frog C come from the same distribution. You will therefore test another, less restrictive hypothesis: The mean strike force of Frog B is equal to that of Frog C.
To set up the bootstrap hypothesis test, you will take the mean as our test statistic. Remember, your goal is to calculate the probability of getting a mean impact force less than or equal to what was observed for Frog B if the hypothesis that the true mean of Frog B's impact forces is equal to that of Frog C is true. You first translate all of the data of Frog B such that the mean is 0.55 N. This involves adding the mean force of Frog C and subtracting the mean force of Frog B from each measurement of Frog B. This leaves other properties of Frog B's distribution, such as the variance, unchanged.
# Make an array of translated impact forces: translated_force_b
translated_force_b = force_b - np.mean(force_b) + 0.55
# Take bootstrap replicates of Frog B's translated impact forces: bs_replicates
bs_replicates = draw_bs_reps(translated_force_b, np.mean, 10000)
# Compute fraction of replicates that are less than the observed Frog B force: p
p = np.sum(bs_replicates <= np.mean(force_b)) / 10000
# Print the p-value
print('p = ', p)
A two-sample bootstrap hypothesis test for difference of means¶
We now want to test the hypothesis that Frog A and Frog B have the same mean impact force, but not necessarily the same distribution, which is also impossible with a permutation test.
To do the two-sample bootstrap test, we shift both arrays to have the same mean, since we are simulating the hypothesis that their means are, in fact, equal. We then draw bootstrap samples out of the shifted arrays and compute the difference in means. This constitutes a bootstrap replicate, and we generate many of them. The p-value is the fraction of replicates with a difference in means greater than or equal to what was observed.
criteria_1 = df_f['ID']=='I'
criteria_2 = df_f['ID']=='II'
criteria_all = criteria_1 & criteria_2
forces_concat = df_f[criteria_all]
forces_concat = df_f['impact force / body weight']
# Compute mean of all forces: mean_force
mean_force = np.mean(forces_concat)
# Generate shifted arrays
force_a_shifted = force_a - np.mean(force_a) + mean_force
force_b_shifted = force_b - np.mean(force_b) + mean_force
# Compute 10,000 bootstrap replicates from shifted arrays
bs_replicates_a = draw_bs_reps(force_a_shifted, np.mean, size=10000)
bs_replicates_b = draw_bs_reps(force_b_shifted, np.mean, size=10000)
# Get replicates of difference of means: bs_replicates
bs_replicates = bs_replicates_a - bs_replicates_b
# Compute and print p-value: p
p = np.sum(bs_replicates >= empirical_diff_means) / len(bs_replicates)
print('p-value =', p)
The vote for the Civil Rights Act in 1964¶
The Civil Rights Act of 1964 was one of the most important pieces of legislation ever passed in the USA. Excluding "present" and "abstain" votes, 153 House Democrats and 136 Republicans voted yea. However, 91 Democrats and 35 Republicans voted nay. Did party affiliation make a difference in the vote?
To answer this question, you will evaluate the hypothesis that the party of a House member has no bearing on his or her vote. You will use the fraction of Democrats voting in favor as your test statistic and evaluate the probability of observing a fraction of Democrats voting in favor at least as small as the observed fraction of 153/244. (That's right, at least as small as. In 1964, it was the Democrats who were less progressive on civil rights issues.) To do this, permute the party labels of the House voters and then arbitrarily divide them into "Democrats" and "Republicans" and compute the fraction of Democrats voting yea.
# Construct arrays of data: dems, reps
dems = np.array([True] * 153 + [False] * 91)
reps = np.array([True] * 136 + [False] * 35)
def frac_yea_dems(dems, reps):
"""Compute fraction of Democrat yea votes."""
frac = np.sum(dems) / len(dems)
return frac
# Acquire permutation samples: perm_replicates
perm_replicates = draw_perm_reps(dems, reps, frac_yea_dems, size=10000)
# Compute and print p-value: p
p = np.sum(perm_replicates <= 153/244) / len(perm_replicates)
print('p-value =', p)
Hypothesis test on Pearson correlation¶
The observed correlation between female illiteracy and fertility may just be by chance; the fertility of a given country may actually be totally independent of its illiteracy. You will test this hypothesis. To do so, permute the illiteracy values but leave the fertility values fixed. This simulates the hypothesis that they are totally independent of each other. For each permutation, compute the Pearson correlation coefficient and assess how many of your permutation replicates have a Pearson correlation coefficient greater than the observed one.
# Compute observed correlation: r_obs
r_obs = pearson_r(illiteracy, fertility)
# Initialize permutation replicates: perm_replicates
perm_replicates = np.empty(10000)
# Draw replicates
for i in range(10000):
# Permute illiteracy measurments: illiteracy_permuted
illiteracy_permuted = np.random.permutation(illiteracy)
# Compute Pearson correlation
perm_replicates[i] = pearson_r(illiteracy_permuted, fertility)
# Compute p-value: p
p = np.sum(perm_replicates >= r_obs) / len(perm_replicates)
print('p-val =', p)