Imbalanced Classes in Your Machine Learning Dataset

What is Imbalanced Data?

Imbalanced data typically refers to a classification problem where the target classes are not represented equally.

For example, you have a 2-class (binary) classification problem with 100 samples. A total of 80 sapmles are labeled with Class-1 and the remaining 20 samples are labeled withClass-2. You are working on your dataset. You create a classification model and get 90% accuracy immediately. “Fantastic” you think. You continue on and go a little deeper and discover that 80% of the data belongs to one class.

This is an imbalanced dataset with a ratio of 80:20 for Class-1 to Class-2 or more concisely 4:1. Imbalanced data can cause you a lot of frustration.

You can have a class imbalance problem on two-class classification problems as well as multi-class classification problems. Most techniques can be used on both.

Imbalanced data is Common

Most classification data sets do not have exactly equal number of instances in each class, but a small difference often does not impact results as much.

There are problems where a class imbalance is not just common, it is expected. For example, in datasets like those that characterize fraudulent transactions are imbalanced. The vast majority of the transactions will be in the “Not-Fraud” class and a very small minority will be in the “Fraud” class.

Another example is customer churn datasets, where the vast majority of customers stay with the service (the “No-Churn” class) and a small minority cancel their subscription (the “Churn” class).

When there is a modest class imbalance like 4:1 in the example above it can cause problems.

Misleading Accuracy

• It is the case where your accuracy measures tell the story that you have excellent accuracy (such as 90%), but the accuracy is only reflecting the underlying majority imbalanced class distribution.

• It is very common, because classification accuracy is often the first measure used when evaluating models on most classification problems.

Defaulting to majority

What is going on in our models when we train on an imbalanced dataset?

The reason we get 90% accuracy on an imbalanced data (with 80% of the instances in Class-1) is because our models look at the data and cleverly decide that the best thing to do is to always predict “Class-1” and achieve higher accuracy.

Tactics To Combat Imbalanced Training Data

Can You Collect More Data?

Collecting more data is almost always overlooked. Can you collect more data? Think about whether you are able to gather more data on your problem. A larger dataset might expose a different and perhaps more balanced perspective on the classes. More examples of minor classes may be useful when resampling your dataset.

Changing The Performance Metric

Accuracy is not the metric to use when working with an imbalanced dataset. There are metrics that have been designed to tell you a more representative story when working with imbalanced classes.

Looking at the following performance measures can give more insight into the accuracy of the model than traditional classification accuracy:

• Confusion Matrix: A breakdown of predictions into a table showing correct predictions (the diagonal) and the types of incorrect predictions made (what classes incorrect predictions were assigned).

• Precision: A measure of a classifiers exactness.

• Recall: A measure of a classifiers completeness.

• F1 Score (or F-score):* A weighted average of precision and recall.

• Kappa (or Cohen’s kappa): Classification accuracy normalized by the imbalance of the classes in the data.

• ROC Curves: Like precision and recall, accuracy is divided into sensitivity and specificity and models can be chosen based on the balance thresholds of these values.

• LogLoss The score summarizes the average difference between two probability distributions. A perfect classifier has a log loss of 0.0, with worse values being positive up to infinity.

• Brier score: The Brier score is focused on the positive class, which for imbalanced classification is the minority class. This makes it more preferable than log loss, which is focused on the entire probability distribution. The Brier score is calculated as the mean squared error between the expected probabilities for the positive class (e.g. 1.0) and the predicted probabilities. A perfect classifier has a Brier score of 0.0.

• G-Mean: Sensitivity and Specificity combined into a single score that balances both concerns.

Resampling Your Dataset

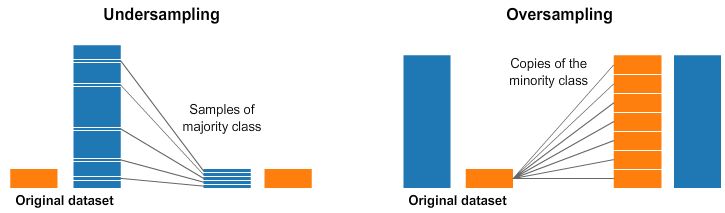
You can change the dataset that you use to build your predictive model to have more balanced data. This change is called sampling your dataset and there are two main methods that you can use to even-up the classes:

You can add copies of instances from the under-represented class called over-sampling (or more formally sampling with replacement), or You can delete instances from the over-represented class, called under-sampling. These approaches are often very easy to implement and fast to run.

Rules of Thumb

• Consider testing under-sampling when you have an a lot data (tens- or hundreds of thousands of instances or more)
• Consider testing over-sampling when you don’t have a lot of data (tens of thousands of records or less)
• Consider testing random and non-random (e.g. stratified) sampling schemes.
• Consider testing different resampled ratios (e.g. you don’t have to target a 1:1 ratio in a binary classification problem, try other ratios)

Generate Synthetic Samples

A simple way to generate synthetic samples is to randomly sample the attributes from instances in the minority class.

There are systematic algorithms that you can use to generate synthetic samples. The most popular of such algorithms is called SMOTE or the Synthetic Minority Over-sampling Technique.

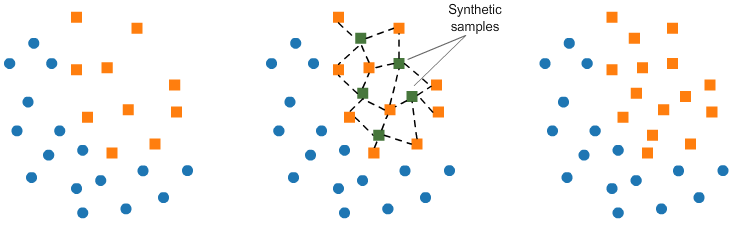
As its name suggests, SMOTE is an oversampling method. It works by creating synthetic samples from the minor class instead of creating copies. The algorithm selects two or more similar instances (using a distance measure) and perturbing an instance one attribute at a time by a random amount within the difference to the neighboring instances.

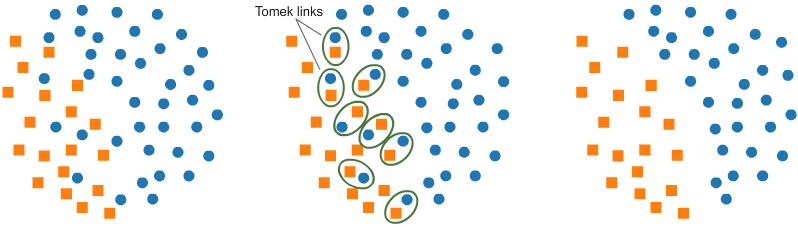
Another resampling algorithm is Tomek links for under-sampling. Tomek links are pairs of very close instances, but of opposite classes. Removing the instances of the majority class of each pair increases the space between the two classes, facilitating the classification process.

Different Algorithms

You should at least be spot-checking a variety of different types of algorithms on a given problem.

That being said, decision trees often perform well on imbalanced datasets. The splitting rules that look at the class variable used in the creation of the trees, can force both classes to be addressed. Try a few popular decision tree algorithms like C4.5, C5.0, CART, XGboost, and Random Forest.

Synthetic binary classification dataset

using the make_classification() function from the scikit-learn library we can for example, we can create 10,000 examples with 2 input variables and a 1:100 distribution as follows:

from sklearn.datasets import make_classification
from collections import Counter
import matplotlib.pyplot as plt
import seaborn as sns
import pandas as pd
import numpy as np

import warnings
warnings.filterwarnings('ignore')

num_features = 12

X, y = make_classification(n_samples=10000, n_features=num_features, n_informative=5, n_redundant=1, n_repeated=0, 
                           n_classes=2, n_clusters_per_class=1, weights=[0.99], flip_y=0, 
                           hypercube=True, shift=0.0, scale=1.0, shuffle=True, random_state=None)

feat_names = ['f'+str(num) for num in list(range(1,1+num_features,1))]

df = pd.DataFrame(X, columns=feat_names)
df['Target'] = y

df.head()

	f1	f2	f3	f4	f5	f6	f7	f8	f9	f10	f11	f12	Target
0	1.483268	-2.332530	1.440274	0.770778	-0.778622	1.565424	0.447782	-0.005006	-0.131874	0.653166	0.185095	0.392335	0
1	-1.028028	0.541285	-0.586828	-1.343240	-0.238558	-1.398803	-0.589714	0.072228	0.357921	0.624001	0.137006	-1.600890	0
2	1.278090	-2.181594	2.923911	-0.248195	-0.056109	1.953303	0.890223	1.333841	-2.382008	-0.199334	1.312382	-0.104277	0
3	2.127533	1.688087	-1.543833	2.749424	0.503071	-0.820361	-1.634686	1.555906	-0.626449	-1.828571	-0.627618	1.532113	0
4	1.121221	-3.807492	3.483039	-1.267689	0.379117	4.396039	2.466005	0.704518	0.317514	-0.098277	-1.302624	-0.586936	0

Plot Data

A scatter plot and count plot is created showing all of the examples in the dataset. We can see a large mass of examples for class 0 (blue) and a small number of examples for class 1 (orange). We can also see that the classes overlap with some examples from class 1 clearly within the part of the feature space that belongs to class 0.

plt.figure(figsize=(8,5))
counter = Counter(y)
for label, _ in counter.items():
    row_ix = np.where(y == label)[0]
    plt.scatter(X[row_ix, 0], X[row_ix, 1], label=str(label), alpha=0.6)
plt.legend()
plt.show()

total = len(df)
plt.figure(figsize=(7,5))
g = sns.countplot(x='Target', data=df)
g.set_ylabel('Count', fontsize=14)
for p in g.patches:
    height = p.get_height()
    g.text(p.get_x()+p.get_width()/2.,
            height + 1.5,
            '{:1.2f}%'.format(height/total*100),
            ha="center", fontsize=14, fontweight='bold')
plt.margins(y=0.1)
plt.show()

Function to train, test and score a RandomForestClassifier

from sklearn.model_selection import train_test_split
from sklearn.metrics import classification_report, confusion_matrix
from sklearn.ensemble import RandomForestClassifier
from yellowbrick.classifier import ConfusionMatrix
from yellowbrick.classifier import ROCAUC
from yellowbrick.classifier import PrecisionRecallCurve
from yellowbrick.classifier import ClassificationReport
from cycler import cycler
from pylab import rcParams 
plt.rcParams['axes.prop_cycle'] = cycler(color='brgy')

def forest_test(X, Y, class_weight=None):
        
    X_Train, X_Test, Y_Train, Y_Test = train_test_split(X, Y, test_size = 0.30, random_state=0)
    
    # Classifier
    trainedforest = RandomForestClassifier(n_estimators=100, class_weight=class_weight).fit(X_Train,Y_Train)

    f, axes = plt.subplots(1,3 ,figsize=(13,4))
    
    preds = trainedforest.predict(X_Test)
    classes = list(df['Target'].unique())
    cm = ConfusionMatrix(
    trainedforest, classes=classes, ax = axes[0],
    label_encoder={0: 'Majority', 1: 'Minority'})
    cm.fit(X_Train, Y_Train)
    cm.score(X_Test, Y_Test)
    axes[0].set_title('Confusion Matrix')
    axes[0].set_xlabel('Predicted Class')
    axes[0].set_ylabel('True Class')
    
    roc = ROCAUC(trainedforest, classes=["Majority", "Minority"], ax = axes[1])
    roc.fit(X_Train, Y_Train)        
    roc.score(X_Test, Y_Test)
    axes[1].set_title('ROC AUC')
    axes[1].grid(False)
    axes[1].legend()
    
    prc = PrecisionRecallCurve(trainedforest, ax = axes[2])
    prc.fit(X_Train, Y_Train)        
    prc.score(X_Test, Y_Test)
    axes[2].set_title('Precision Recall Curve')
    axes[2].grid(False)
    axes[2].legend()
    
    plt.tight_layout()
    plt.show();

    print('\n',classification_report(Y_Test,preds))

Initial test on unchanged class distribution

forest_test(X, y, class_weight=None)

               precision    recall  f1-score   support

           0       0.99      1.00      1.00      2968
           1       0.88      0.22      0.35        32

    accuracy                           0.99      3000
   macro avg       0.93      0.61      0.67      3000
weighted avg       0.99      0.99      0.99      3000

Imbalanced-Learn Library

In these examples, we will use the implementations provided by the imbalanced-learn Python library.

Tomek Links for under sampling

from imblearn.under_sampling import TomekLinks

# define the undersampling method
undersample = TomekLinks()

# transform the dataset
X1, y1 = undersample.fit_resample(X, y)

# summarize the new class distribution
counter = Counter(y)

# scatter plot of examples by class label
for label, _ in counter.items():
    row_ix = np.where(y1 == label)[0]
    plt.scatter(X1[row_ix, 0], X1[row_ix, 1], label=str(label), alpha=0.6)
plt.legend()
plt.show()

df1 = pd.DataFrame(X1, columns=feat_names)
df1['Target'] = y1

total = len(df)
plt.figure(figsize=(7,5))
g = sns.countplot(x='Target', data=df1)
g.set_ylabel('Count', fontsize=14)
for p in g.patches:
    height = p.get_height()
    g.text(p.get_x()+p.get_width()/2.,
            height + 1.5,
            '{:1.2f}%'.format(height/total*100),
            ha="center", fontsize=14, fontweight='bold')
plt.margins(y=0.1)
plt.show()

Using TensorFlow backend.

forest_test(X1, y1, class_weight=None)

               precision    recall  f1-score   support

           0       0.99      1.00      1.00      2969
           1       1.00      0.24      0.39        29

    accuracy                           0.99      2998
   macro avg       1.00      0.62      0.69      2998
weighted avg       0.99      0.99      0.99      2998

Condensed Nearest Neighbour for under sampling

Condensed Nearest Neighbors, or CNN for short, is an undersampling technique that seeks a subset of a collection of samples that results in no loss in model performance, referred to as a minimal consistent set.

• The notion of a consistent subset of a sample set. This is a subset which, when used as a stored reference set for the NN rule, correctly classifies all of the remaining points in the sample set.

When used for imbalanced classification, the store is comprised of all examples in the minority set and only examples from the majority set that cannot be classified correctly are added incrementally to the store.

During the procedure, the KNN algorithm is used to classify points to determine if they are to be added to the store or not. The k value is set via the n_neighbors argument and defaults to 1.

from imblearn.under_sampling import CondensedNearestNeighbour

# define the undersampling method
undersample = CondensedNearestNeighbour(n_neighbors=1)

# transform the dataset
X1, y1 = undersample.fit_resample(X, y)

# summarize the new class distribution
counter = Counter(y)

# scatter plot of examples by class label
for label, _ in counter.items():
    row_ix = np.where(y1 == label)[0]
    plt.scatter(X1[row_ix, 0], X1[row_ix, 1], label=str(label), alpha=0.6)
plt.legend()
plt.show()

df1 = pd.DataFrame(X1, columns=feat_names)
df1['Target'] = y1

total = len(df)
plt.figure(figsize=(7,5))
g = sns.countplot(x='Target', data=df1)
g.set_ylabel('Count', fontsize=14)
for p in g.patches:
    height = p.get_height()
    g.text(p.get_x()+p.get_width()/2.,
            height + 1.5,
            '{:1.2f}%'.format(height/total*100),
            ha="center", fontsize=14, fontweight='bold')
plt.margins(y=0.1)
plt.show()

forest_test(X1, y1, class_weight=None)

               precision    recall  f1-score   support

           0       0.82      0.95      0.88       107
           1       0.67      0.31      0.43        32

    accuracy                           0.81       139
   macro avg       0.74      0.63      0.65       139
weighted avg       0.79      0.81      0.78       139

SMOTE for over sampling

from imblearn.over_sampling import SMOTE

# define the oversampling method
oversample = SMOTE()

# transform the dataset
X1, y1 = oversample.fit_resample(X, y)

# summarize the new class distribution
counter = Counter(y)

# scatter plot of examples by class label
for label, _ in counter.items():
    row_ix = np.where(y1 == label)[0]
    plt.scatter(X1[row_ix, 0], X1[row_ix, 1], label=str(label), alpha=0.6)
plt.legend()
plt.show()

df1 = pd.DataFrame(X1, columns=feat_names)
df1['Target'] = y1

total = len(df)
plt.figure(figsize=(7,5))
g = sns.countplot(x='Target', data=df1)
g.set_ylabel('Count', fontsize=14)
for p in g.patches:
    height = p.get_height()
    g.text(p.get_x()+p.get_width()/2.,
            height + 1.5,
            '{:1.2f}%'.format(height/total*100),
            ha="center", fontsize=14, fontweight='bold')
plt.margins(y=0.1)
plt.show()

forest_test(X1, y1, class_weight=None)

               precision    recall  f1-score   support

           0       1.00      1.00      1.00      2973
           1       1.00      1.00      1.00      2967

    accuracy                           1.00      5940
   macro avg       1.00      1.00      1.00      5940
weighted avg       1.00      1.00      1.00      5940

Penalized Models

Penalized classification imposes an additional cost on the model for making classification mistakes on the minority class during training. These penalties can bias the model to pay more attention to the minority class (cost sensitive).

Often the handling of class penalties or weights are specialized to the learning algorithm. There are penalized versions of algorithms such as penalized-SVM and penalized-LDA.

Using penalization is desirable if you are locked into a specific algorithm and are unable to resample or you’re getting poor results. It provides yet another way to “balance” the classes. Setting up the penalty matrix can be complex. You will very likely have to try a variety of penalty schemes and see what works best for your problem.

Random Forest With Class Weighting

A simple technique for modifying a decision tree for imbalanced classification is to change the weight that each class has when calculating the “impurity” score of a chosen split point.

Impurity measures how mixed the groups of samples are for a given split in the training dataset and is typically measured with Gini or entropy. The calculation can be biased so that a mixture in favor of the minority class is favored, allowing some false positives for the majority class.

This modification of random forest is referred to as Weighted Random Forest. This can be achieved by setting the class_weight argument on the RandomForestClassifier class.

This argument takes a dictionary with a mapping of each class value (e.g. 0 and 1) to the weighting. The argument value of ‘balanced‘ can be provided to automatically use the inverse weighting from the training dataset, giving focus to the minority class.

forest_test(X, y, class_weight='balanced')

               precision    recall  f1-score   support

           0       0.99      1.00      1.00      2968
           1       0.89      0.25      0.39        32

    accuracy                           0.99      3000
   macro avg       0.94      0.62      0.69      3000
weighted avg       0.99      0.99      0.99      3000

Random Forest With Bootstrap Class Weighting

Given that each decision tree is constructed from a bootstrap sample (e.g. random selection with replacement), the class distribution in the data sample will be different for each tree.

As such, it might be interesting to change the class weighting based on the class distribution in each bootstrap sample, instead of the entire training dataset.

This can be achieved by setting the class_weight argument to the value ‘balanced_subsample‘.

forest_test(X, y, class_weight='balanced_subsample')

               precision    recall  f1-score   support

           0       0.99      1.00      1.00      2968
           1       0.88      0.22      0.35        32

    accuracy                           0.99      3000
   macro avg       0.93      0.61      0.67      3000
weighted avg       0.99      0.99      0.99      3000

Random Forest With Custom Class Weighting

Say the class distribution of the test dataset is a 1:10 ratio for the minority class to the majority class. The invert of this ratio could be used with 1 for the majority class and 10 for the minority class; for example:

weights = {0:1, 1:10}
forest_test(X, y, class_weight=weights)

               precision    recall  f1-score   support

           0       0.99      1.00      1.00      2968
           1       1.00      0.22      0.36        32

    accuracy                           0.99      3000
   macro avg       1.00      0.61      0.68      3000
weighted avg       0.99      0.99      0.99      3000

Cost-Sensitive Neural Network for Imbalanced Classification

Neural network models are commonly trained using the backpropagation of error algorithm.

This involves using the current state of the model to make predictions for training set examples, calculating the error for the predictions, then updating the model weights using the error, and assigning credit for the error to different nodes and layers backward from the output layer back through to the input layer.

Given the balanced focus on misclassification errors, most standard neural network algorithms are not well suited to datasets with a severely skewed class distribution. This training procedure can be modified so that some examples have more or less error than others.

The simplest way to implement this is to use a fixed weighting of error scores for examples based on their class where the prediction error is increased for examples in a more important class and decreased or left unchanged for those examples in a less important class.

A large error weighting can be applied to those examples in the minority class as they are often more important in an imbalanced classification problem than examples from the majority class.

• Large Weight: Assigned to examples from the minority class.
• Small Weight: Assigned to examples from the majority class.

This modification to the neural network training algorithm is referred to as a Weighted Neural Network or Cost-Sensitive Neural Network.

Typically, careful attention is required when defining the costs or “weightings” to use for cost-sensitive learning. However, for imbalanced classification where only misclassification is the focus, the weighting can use the inverse of the class distribution observed in the training dataset.

# prepare train and test dataset
def prepare_data():
    # split into train and test
    X_Train, X_Test, y_Train, y_Test = train_test_split(X, y, test_size = 0.30, random_state=420)
    return X_Train, X_Test, y_Train, y_Test

from keras.models import Sequential
from keras.layers import Dense
from sklearn.metrics import roc_auc_score

# define the neural network model
def define_model(n_input):
    # define model
    model = Sequential()
    # define first hidden layer and visible layer
    model.add(Dense(10, input_dim=n_input, activation='relu', kernel_initializer='he_uniform'))
    # define output layer
    model.add(Dense(1, activation='sigmoid'))
    # define loss and optimizer
    model.compile(loss='binary_crossentropy', optimizer='sgd')
    return model

# prepare dataset
X_Train, X_Test, y_Train, y_Test = prepare_data()

# define the model
n_input = X_Train.shape[1]
model = define_model(n_input)

# fit model
model.fit(X_Train, y_Train, epochs=100, verbose=0)

# make predictions on the test dataset
yhat = model.predict(X_Test)

# evaluate the ROC AUC of the predictions
score = roc_auc_score(y_Test, yhat)
print(f'ROC AUC: {score}')

ROC AUC: 0.831009953781565

The fit() function that is used to train Keras neural network models takes an argument called class_weight. This argument allows you to define a dictionary that maps class integer values to the importance to apply to each class.

This function is used to train each different type of neural network, including Multilayer Perceptrons, Convolutional Neural Networks, and Recurrent Neural Networks, therefore the class weighting capability is available for those network types.

For example, a 1 to 1 weighting for each class 0 and 1 can be defined as follows:

# fit model
weights = {0:1, 1:1}
history = model.fit(X_Train, y_Train, class_weight=weights, epochs=100, verbose=0)

# evaluate model
yhat = model.predict(X_Test)
score = roc_auc_score(y_Test, yhat)
print('ROC AUC: %.3f' % score)

ROC AUC: 0.854

The class weighing can be defined multiple ways:

• Domain expertise, determined by talking to subject matter experts.
• Tuning, determined by a hyperparameter search such as a grid search.
• Heuristic, specified using a general best practice.

A best practice for using the class weighting is to use the inverse of the class distribution present in the training dataset.

For example, the class distribution of the test dataset is a 1:100 ratio for the minority class to the majority class. The invert of this ratio could be used with 1 for the majority class and 100 for the minority class, for example:

# fit model
weights = {0:1, 1:100}
history = model.fit(X_Train, y_Train, class_weight=weights, epochs=100, verbose=0)

# evaluate model
yhat = model.predict(X_Test)
score = roc_auc_score(y_Test, yhat)
print('ROC AUC: %.3f' % score)

ROC AUC: 0.883

Fractions that represent the same ratio do not have the same effect. For example, using 0.01 and 0.99 for the majority and minority classes respectively may result in worse performance than using 1 and 100.

# fit model
weights = {0:0.01, 1:0.99}
history = model.fit(X_Train, y_Train, class_weight=weights, epochs=100, verbose=0)

# evaluate model
yhat = model.predict(X_Test)
score = roc_auc_score(y_Test, yhat)
print('ROC AUC: %.3f' % score)

ROC AUC: 0.888

Try a Different Perspective

• Anomaly detection is the detection of rare events. This might be a machine malfunction indicated through its vibrations or a malicious activity by a program indicated by it’s sequence of system calls. The events are rare and when compared to normal operation.

This shift in thinking considers the minor class as the outliers class which might help you think of new ways to separate and classify samples.

• Change detection is similar to anomaly detection except rather than looking for an anomaly it is looking for a change or difference. This might be a change in behavior of a user as observed by usage patterns or bank transactions.

Both of these shifts take a more real-time stance to the classification problem that might give you some new ways of thinking about your problem and maybe some more techniques to try.