Fama–MacBeth regression¶
Given data on risk factors and portfolio returns, it is useful to estimate the portfolio's exposure, or how much a risk factor is driving portfolio returns, as well as how much is the exposure to a given risk factor worth. What is the market's risk factor premium?
The risk premium then permits to estimate the return for any portfolio provided the factor exposure is known or can be estimated.
More formally, we will have i=1, ..., N asset or portfolio returns over t=1, ..., T periods and each asset's excess period return will be denoted. The goals is to test whether the j=1, ...,M factors explain the excess returns and the risk premium associated with each risk factor. In our case, we have N=17 portfolios and M=5risk factors, each with =120 periods of data.
Inference problems will likely arise in such cross-sectional regressions because the fundamental assumptions of classical linear regression may not hold. Potential violations include measurement errors, covariation of residuals due to heteroskedasticity and serial correlation, and multicollinearity.
To address the inference problem caused by the correlation of the residuals, Fama and MacBeth proposed a two step methodology for a cross-sectional regression of returns on risk factors. The two-stage Fama—Macbeth regression is designed to estimate the premium rewarded for the exposure to a particular risk factor by the market. The two stages consist of:
- First stage:
Ntime-series regression, one for each asset or portfolio, of its excess returns on the factors to estimate the factor loadings. In matrix form, for each asset:
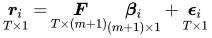
- Second stage:
Tcross-sectional regression, one for each time period, to estimate the risk premium. In matrix form, we obtain a vector $\hat{\lambda_t}$ of risk premia for each period:
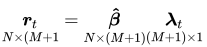
Now we can compute the factor risk premia as the time average and get t-statistic to assess their individual significance, using the assumption that the risk premia estimates are
independent over time:
Why build a linear factor model?¶
Algorithmic trading strategies use linear factor models to quantify the relationship between the return of an asset and the sources of risk that represent the main drivers of these returns. Each factor risk carries a premium, and the total asset return can be expected to correspond to a weighted average of these risk premia.
There are several practical applications of factor models across the portfolio management process from construction and asset selection to risk management and performance evaluation. The importance of factor models continues to grow as common risk factors are now tradeable:
- A summary of the returns of many assets by a much smaller number of factors reduces the amount of data required to estimate the covariance matrix when optimizing a portfolio
- An estimate of the exposure of an asset or a portfolio to these factors allows for the management of the resultant risk, for instance by entering suitable hedges when risk factors are themselves traded
- A factor model also permits the assessment of the incremental signal content of new alpha factors
- A factor model can also help assess whether a manager's performance relative to a benchmark is indeed due to skill in selecting assets and timing the market, or if instead, the performance can be explained by portfolio tilts towards known return drivers that can today be replicated as low-cost, passively managed funds without incurring active management fees
Imports¶
from pprint import pprint
import numpy as np
import pandas as pd
import pyfolio as pf
import quantstats as qs
from datetime import date
from pandas_datareader.famafrench import get_available_datasets
from scipy.stats import spearmanr, pearsonr
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import matplotlib.cm as cm
from statsmodels.api import OLS, add_constant
from pathlib import Path
from linearmodels.asset_pricing import TradedFactorModel, LinearFactorModel, LinearFactorModelGMM
import nance_db
import seaborn as sns
from pandas_datareader import data as web
import warnings
warnings.filterwarnings('ignore')
pd.set_option('display.max_columns', None)
pd.set_option('display.max_rows', 500)
Get Data¶
Fama and French make updated risk factor and research portfolio data available through their website, and you can use the pandas_datareader package to obtain the data.
Risk Factors¶
We will be using the five Fama—French factors that result from sorting stocks first into three size groups and then into two for each of the remaining three firm-specific factors.
Hence, the factors involve three sets of value-weighted portfolios formed as 3 x 2 sorts on size and book-to-market, size and operating profitability, and size and investment. The risk factor values are computed as the average returns of the portfolios (PF) as outlined in the following table:
| Label | Name | Description |
|---|---|---|
| SMB | Small Minus Big | Average return on the nine small stock portfolios minus the average return on the nine big stock portfolios |
| HML | High Minus Low | Average return on the two value portfolios minus the average return on the two growth portfolios |
| RMW | Robust minus Weak | Average return on the two robust operating profitability portfolios minus the average return on the two weak operating profitability portfolios |
| CMA | Conservative Minus Aggressive | Average return on the two conservative investment portfolios minus the average return on the two aggressive investment portfolios |
| Rm-Rf | Excess return on the market | Value-weight return of all firms incorporated in the US and listed on the NYSE, AMEX, or NASDAQ at the beginning of month t with 'good' data for t minus the one-month Treasury bill rate |
The Fama-French 5 factors are based on the 6 value-weight portfolios formed on size and book-to-market, the 6 value-weight portfolios formed on size and operating profitability, and the 6 value-weight portfolios formed on size and investment.
We will use returns at a monthly frequency that we obtain for the period 2010 – 2020 as follows:
start = pd.Timestamp('2010')
end = pd.Timestamp('2020-02')
ff_factor = 'F-F_Research_Data_5_Factors_2x3'
ff_factor_data = web.DataReader(ff_factor, 'famafrench', start=start, end=end)[0]
ff_factor_data.info()
ff_factor_data.describe()
Portfolios¶
Fama and French also make numerous portfolios that we can illustrate the estimation of the risk factor exposures, as well as the value of the risk premia available in the market for a given time period. We will use a panel of the 17 industry portfolios at a monthly frequency.
We will subtract the risk-free rate from the returns because the factor model works with excess returns:
ff_portfolio = '17_Industry_Portfolios'
ff_portfolio_data = web.DataReader(ff_portfolio, 'famafrench', start=start, end=end)[0]
ff_portfolio_data = ff_portfolio_data.sub(ff_factor_data.RF, axis=0)
ff_portfolio_data.info()
Equity Data¶
Vanguard Sector & specialty ETFs
symbols = ['VOX', 'VCR', 'VDC', 'VDE', 'VFH', 'VHT', 'VIS', 'VGT', 'VAW', 'VNQ', 'VPU']
secs = ['COMM', 'CONSUMER DISC', 'CONSUMER ST', 'ENERGY', 'FINANCIALS', 'HEALTH', 'INDUSTRIALS',
'TECHNOLOGY', 'MATIREALS', 'REAL ESTATE', 'UTILITIES']
def get_symbols(symbols,data_source,ohlc,begin_date=None,end_date=None):
out = []
new_symbols = []
for symbol in symbols:
df = web.DataReader(symbol, data_source,begin_date, end_date)\
[['High','Low','Open','Close','Volume','Adj Close']]
new_symbols.append(symbol)
out.append(df[ohlc].astype('float'))
data = pd.concat(out, axis = 1)
data.columns = new_symbols
return data
prices = get_symbols(symbols,data_source='yahoo',ohlc='Close',\
begin_date=start,end_date=end)
SPY = web.DataReader('SPY', 'yahoo', start, end)\
[['High','Low','Open','Close','Volume','Adj Close']]
prices.columns = secs
prices['SPY'] = SPY.Close.values
prices.info()
returns0 = prices.pct_change()
returns0 = returns0.dropna(how='all').dropna(axis=1)
EDA¶
pricesx = returns0.copy()
n_secs = len(pricesx.columns)
colors = cm.rainbow(np.linspace(0, 1, n_secs))
pricesx.cumsum().plot(color=colors, figsize=(12, 6))# Normalize Prices
plt.title('Cummulative Returns Series')
plt.xlabel('Date')
plt.ylabel('Returns (%)')
plt.grid(b=None, which=u'major', axis=u'both')
plt.legend(bbox_to_anchor=(1.01, 1.1), loc='upper left', ncol=1)
plt.show();
pricesx.hist(bins=20, figsize=(10,10))
plt.tight_layout()
plt.show()
plt.figure(figsize=(12,6))
g1 = sns.boxplot(data=pricesx)
g1.set_xticklabels(g1.get_xticklabels(),rotation=90)
plt.title('Returns')
plt.tight_layout()
plt.show()
plt.figure(figsize=(12,6))
pricesx.mean().sort_values(ascending=True).plot(kind='barh',colors=colors)
plt.title('Mean Return')
plt.tight_layout()
plt.show()
g = sns.clustermap(pricesx.corr(), annot=True)
ax = g.ax_heatmap
bottom, top = ax.get_ylim()
ax.set_ylim(bottom + 0.5, top - 0.5)
plt.title('Pairwise Correlations')
plt.show()
pricesx.drop('SPY', axis=1).rolling(63).corr(pricesx.SPY).dropna().plot(color=colors, figsize=(12, 6))
plt.legend(bbox_to_anchor=(1.01, 1.1), loc='upper left', ncol=1)
plt.title('Rolling Quarterly Correlation to SPY')
plt.show()
pricesx.drop('SPY',axis=1).corrwith(pricesx.SPY).sort_values(ascending=True).plot(kind='barh', color=colors, figsize=(12, 6))
plt.title('Correlation to SPY')
plt.show()
pricesx.rolling(63).var().dropna().plot(color=colors, figsize=(12, 6))
plt.legend(bbox_to_anchor=(1.01, 1.1), loc='upper left', ncol=1)
plt.title('Rolling Quarterly Variance')
plt.show()
plt.figure(figsize=(12,6))
g2 = sns.boxplot(data=pricesx.rolling(63).std().dropna())
g2.set_xticklabels(g2.get_xticklabels(),rotation=90)
plt.title('Rolling Quarterly Returns Volatility')
plt.tight_layout()
plt.show()
plt.figure(figsize=(12,6))
pricesx.std().sort_values(ascending=True).plot(kind='barh',colors=colors)
plt.title('Returns Volatility')
plt.tight_layout()
plt.show()
def r2(x, y):
return pearsonr(x, y)[0] ** 2
tmp_fts = pricesx.copy()
fig, axs = plt.subplots(ncols=2, nrows=0, figsize=(10, 40))
plt.subplots_adjust(right=2.5)
plt.subplots_adjust(top=2)
cm = plt.get_cmap('jet')
colors = np.linspace(0.1, 1, len(tmp_fts))
for i, feature in enumerate(list(tmp_fts), 1):
if(feature=='SPY'):
break
ic, pval = spearmanr(tmp_fts[feature], tmp_fts['SPY'])
R2 = r2(tmp_fts[feature], tmp_fts['SPY'])
plt.subplot(len(list(tmp_fts.columns)), 3, i)
sc = plt.scatter(tmp_fts[feature], tmp_fts['SPY'], s=200,
edgecolor='k', alpha=0.5, label='Price Data', c=colors, cmap=cm)
j = sns.regplot(tmp_fts[feature], tmp_fts['SPY'], data=tmp_fts, scatter=False, label=False,
line_kws={'color':'k','lw':2.5, 'alpha':0.65})
plt.ylabel('SPY', size=23, labelpad=14, fontsize=20, fontweight='medium')
plt.title(f'{feature}: r2 = {round(R2,2)}', fontsize=23, fontweight='medium')
plt.grid(False)
for j in range(2):
plt.tick_params(axis='x', labelsize=20)
plt.tick_params(axis='y', labelsize=20)
plt.show()
returns = prices.resample('M').last().pct_change().mul(100).to_period('M')
returns = returns.dropna(how='all').dropna(axis=1)
returns.info()
Align data¶
ff_factor_data = ff_factor_data.loc[returns.index]
ff_portfolio_data = ff_portfolio_data.loc[returns.index]
ff_factor_data.describe()
Compute excess Returns¶
excess_returns = returns.sub(ff_factor_data.RF, axis=0)
excess_returns.info()
excess_returns = excess_returns.clip(lower=np.percentile(excess_returns, 1),
upper=np.percentile(excess_returns, 99))
Fama-Macbeth Regression¶
Given data on risk factors and portfolio returns, it is useful to estimate the portfolio's exposure, that is, how much the risk factors drive portfolio returns, as well as how much the exposure to a given factor is worth, that is, the what market's risk factor premium is. The risk premium then permits to estimate the return for any portfolio provided the factor exposure is known or can be assumed.
ff_portfolio_data.info()
ff_factor_data.info()
Factor Exposures¶
We can implement the first stage to obtain the 17 factor loading estimates as follows:
from statsmodels.api import OLS, add_constant
betas = []
for industry in ff_portfolio_data:
step1 = OLS(endog=ff_portfolio_data.loc[ff_factor_data.index, industry],
exog=add_constant(ff_factor_data)).fit()
betas.append(step1.params.drop('const'))
betas = pd.DataFrame(betas,
columns=ff_factor_data.columns,
index=ff_portfolio_data.columns)
betas.info()
Risk Premia¶
For the second stage, we run 120 regressions of the period returns for the cross section of portfolios on the factor loadings
lambdas = []
for period in ff_portfolio_data.index:
step2 = OLS(endog=ff_portfolio_data.loc[period, betas.index],
exog=betas).fit()
lambdas.append(step2.params)
lambdas = pd.DataFrame(lambdas,
index=ff_portfolio_data.index,
columns=betas.columns.tolist())
lambdas.info()
lambdas.mean()
ax1 = plt.subplot2grid((1, 3), (0, 0))
ax2 = plt.subplot2grid((1, 3), (0, 1), colspan=2)
ax2.margins(0.01)
lambdas.mean().plot.barh(ax=ax1)
lambdas0 = lambdas.rolling(6).mean().dropna()
lambdas0.plot(lw=2, figsize=(17,8), ax=ax2)
ax2.legend(bbox_to_anchor=(1.025, 1.05))
plt.show()
lambdas.rolling(12).mean().dropna().plot(lw=2, figsize=(14,20), subplots=True, sharey=True, sharex=True)
plt.show()
Fama-Macbeth with the LinearModels library¶
The linear_models library extends statsmodels with various models for panel data and also implements the two-stage Fama—MacBeth procedure:
from linearmodels.asset_pricing import TradedFactorModel, LinearFactorModel, LinearFactorModelGMM
mod = LinearFactorModel(portfolios=ff_portfolio_data,
factors=ff_factor_data)
res = mod.fit(cov_type='robust')
print(res.summary)
This provides us with the same result:
lambdas.mean()