Decision trees¶
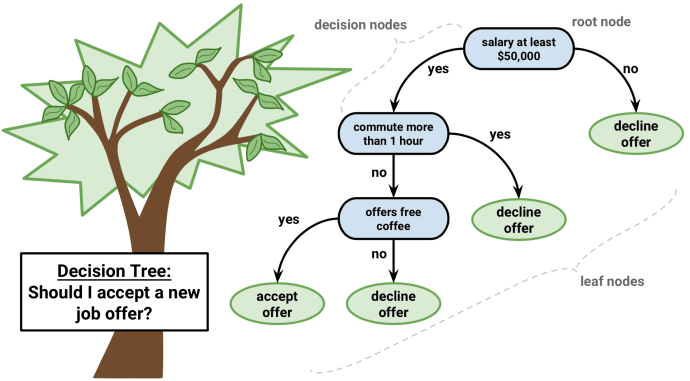
Decision trees are a machine learning algorithm that predicts the value of a target variable based on decision rules learned from training data. The algorithm can be applied to both regression and classification problems by changing the objective function that governs how the tree learns the decision rules.
How trees learn and apply decision rules¶
Decision trees learn and sequentially apply a set of rules that split data points into subsets and then make one prediction for each subset. The predictions are based on the outcome values for the subset of training samples that result from the application of a given sequence of rules.
The root is the starting point for all samples, nodes represent the application of the decision rules, and the data moves along the edges as it is split into smaller subsets until arriving at a leaf node where the model makes a prediction.
Each of these rules relies on one particular feature and uses a threshold to split the samples into two groups with values either below or above the threshold with respect to this feature.
During training, the algorithm scans the features and, for each feature, seeks to find a cutoff that splits the data to minimize the loss that results from predictions made using the subsets that would result from the split, weighted by the number of samples in each subset.
Classification trees predict a probability estimated from the relative class frequencies or the value of the majority class directly.
Regression models compute prediction from the mean of the outcome values for the available data points.
Building Blocks of a Decision-Tree¶
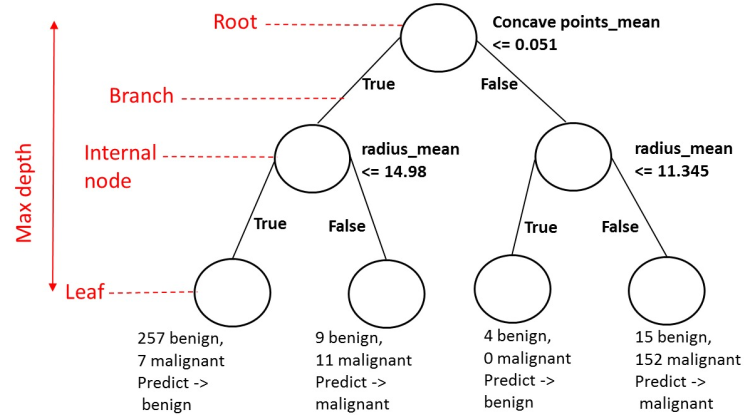
- Node: question or prediction
Three kinds of nodes:
- Root: no parent node, question giving rise to two children nodes.
- Internal node: one parent node, question giving rise to two children nodes.
- Leaf: one parent node, no children nodes --> prediction.
Tree-based learning takes a top-down, greedy approach, known as recursive binary splitting.¶
- This process is recursive because it uses subsets of data resulting from prior splits.
- It is top-down because it begins at the root node of the tree, where all observations still belong to a single region and then successively creates two new branches of the tree by adding one more split to the predictor space.
- It is greedy because the algorithm picks the best rule in the form of a feature-threshold combination based on the immediate impact on the objective function rather than looking ahead and evaluating the loss several steps ahead.
The number of training samples gradually shrinks as recursive splits add new nodes to the tree. If rules split the samples evenly, resulting in a perfectly balanced tree with an $n$ equal number of children for every node, then there would be $2^n$ nodes at level $n$, each containing a corresponding fraction of the total number of observations. This is unlikely, so the number of samples along some branches may diminish rapidly, and trees tend to grow to different levels of depth along different paths.
To arrive at a prediction for a new observation, the model uses the rules that it inferred during training to decide which leaf node the data point should be assigned to. A smaller number of training samples in a given region of the feature space or leaf node, reduces the confidence in the prediction and may be overfitting.
- Splitting rules:
- mean (for regression)
- mode (for classification)
Recursive splitting continues until each leaf node contains only a single sample and the training error has been reduced to zero.
How to use decision trees in practice¶
To demonstrate regression trees we predict returns
To demonstrate the classification case, we predict positive and negative asset price moves
Imports¶
%matplotlib inline
import warnings
import os
from pathlib import Path
import quandl
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from matplotlib.ticker import FuncFormatter
from matplotlib import cm
import seaborn as sns
import graphviz
from IPython.display import Image
import pydotplus
from IPython.display import Image
from sklearn.tree import DecisionTreeClassifier, DecisionTreeRegressor, export_graphviz, _tree
from sklearn.linear_model import LinearRegression, Ridge, LogisticRegression
from sklearn.model_selection import train_test_split, cross_val_score, GridSearchCV, learning_curve, KFold
from sklearn.metrics import roc_auc_score, roc_curve, mean_squared_error, precision_recall_curve, accuracy_score
import statsmodels.api as sm
from scipy.interpolate import interp1d, interp2d
warnings.filterwarnings('ignore')
pd.set_option('display.max_columns', None)
plt.style.use('fivethirtyeight')
Get Data¶
The data consists of daily stock prices for the $2010$-$2020$-$02$ period and various engineered features.
- The decision tree models here are not equipped to handle missing or categorical variables, so we applied dummy encoding to the latter after dropping any of the former.
- We also removed outliers for our response variable keeping data points in between the $5\%$ and $95\%$ quantiles respectively.
with pd.HDFStore('data.h5') as store:
data = store['data']
data.info()
data.head()
Stock Prices¶
y = data.returns
X = data.drop('returns', axis=1)
Binary Outcome¶
y_binary = (y>0).astype(int)
2 Lags Only¶
X2 = X.loc[:, ['t-1', 't-2']]
X2.info()
Explore Data¶
plt.hist(y, bins=50, rwidth=0.8, alpha=0.5);
y.describe(percentiles=np.arange(.1, .91, .1).round(1))
total = len(y_binary)
plt.figure(figsize=(7,5))
g = sns.countplot(x=y_binary.values)
g.set_ylabel('Count', fontsize=14)
for p in g.patches:
height = p.get_height()
g.text(p.get_x()+p.get_width()/2.,
height + 1.5,
'{:1.2f}%'.format(height/total*100),
ha="center", fontsize=14, fontweight='bold')
plt.margins(y=0.1)
plt.title('Y Binary')
plt.show()
Custom KFold¶
Custom cross-validation class tailored to the format of the data just created, which has pandas MultiIndex with two levels, one for the ticker and one for the data.
OneStepTimeSeriesSplit ensures a split of training and validation sets that avoids a lookahead bias by training models using only data up to period $T-1$ for each stock when validating using data for month $T$. We will only use one-step-ahead forecasts.
class OneStepTimeSeriesSplit():
def __init__(self, n_splits=3, test_period_length=1, shuffle=False):
self.n_splits = n_splits
self.test_period_length = test_period_length
self.shuffle = shuffle
self.test_end = n_splits * test_period_length
@staticmethod
def chunks(l, chunk_size):
for i in range(0, len(l), chunk_size):
yield l[i:i + chunk_size]
def split(self, X, y=None, groups=None):
unique_dates = (X.index
.get_level_values('date')
.unique()
.sort_values(ascending=False)[:self.test_end])
dates = X.reset_index()[['date']]
for test_date in self.chunks(unique_dates, self.test_period_length):
train_idx = dates[dates.date < min(test_date)].index
test_idx = dates[dates.date.isin(test_date)].index
if self.shuffle:
np.random.shuffle(list(train_idx))
yield train_idx, test_idx
def get_n_splits(self, X, y, groups=None):
return self.n_splits
Functions to return an evaluation metric for a classifier or regressor using the custom cv class¶
def regression_benchmark():
rmse = []
for train_idx, test_idx in cv.split(X):
mean = y.iloc[train_idx].mean()
data = y.iloc[test_idx].to_frame('y_test').assign(y_pred=mean)
rmse.append(np.sqrt(mean_squared_error(data.y_test, data.y_pred)))
return np.mean(rmse)
def classification_benchmark():
auc = []
for train_idx, test_idx in cv.split(X):
mean = y_binary.iloc[train_idx].mean()
data = y_binary.iloc[test_idx].to_frame('y_test').assign(y_pred=mean)
auc.append(roc_auc_score(data.y_test, data.y_pred))
return np.mean(auc)
View CV Dates & Sizes¶
tss = OneStepTimeSeriesSplit(n_splits=12)
count = 0
for tr_idx, val_idx in tss.split(X2, y):
count += 1
if count == 4:
break
X_tr, X_vl = X2.iloc[tr_idx], X2.iloc[val_idx]
print(f'{len(X_tr)} data points for training:')
print(X_tr.info())
print()
print(f'{len(X_vl)} data points for testing:')
print(X_vl.info())
print()
Simple Regression Tree¶
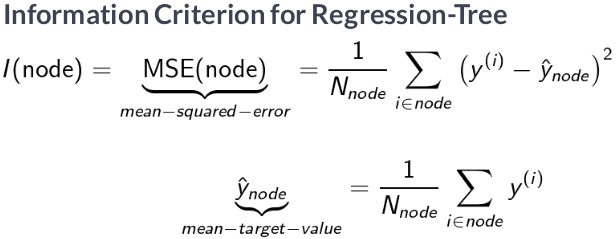
Regression trees make predictions based on the mean outcome value for the training samples assigned to a given node and typically rely on the mean-squared error (MSE) to select optimal rules during recursive binary splitting.
Given a training set, the algorithm iterates over the predictors, $X_1, X_2, ..., X_p$, and possible cutpoints, $s_1, s_2, ..., s_N$, to find an optimal combination. The optimal rule splits the feature space into two regions, $\{X\mid X_i < s_j\}$ and $\{X\mid X_i > s_j\}$, with values for the $X_i$ feature either below or above the $s_j$ threshold so that predictions based on the training subsets maximize the reduction of the squared residuals relative to the current node.
Configure Tree¶
We start with a simplified example to facilitate visualization and only use $2$ months of lagged returns to predict the following month, similar to an $AR(2)$ model.
reg_tree_t2 = DecisionTreeRegressor(criterion='mse',
splitter='best',
max_depth=4,
min_samples_split=2,
min_samples_leaf=1,
min_weight_fraction_leaf=0.0,
max_features=None,
random_state=804,
max_leaf_nodes=None,
min_impurity_decrease=0.0,
min_impurity_split=None,
presort=False)
Train/fit Decision Tree¶
reg_tree_t2.fit(X=X2, y=y)
Visualize Tree¶
- We visualize the tree using the
graphvizlibrary becausesklearncan output a description of the tree using the.dotlanguage used by that library.
- You can configure the output to include feature and class labels and limit the number of levels to keep the chart readable, as follows:
dot_data = export_graphviz(reg_tree_t2,
out_file=None,
feature_names=X2.columns,
max_depth=2,
filled=True,
rounded=True,
special_characters=True)
# Draw graph
graph = pydotplus.graph_from_dot_data(dot_data)
# Show graph
Image(graph.create_png())
Save image¶
# Create PDF
# graph.write_pdf("iris.pdf")
# Create PNG
graph.write_png("reg_tree_t2.png")
Compare with Linear Regression¶
The OLS summary below and a visualization of the first two levels of the decision tree above reveal the striking differences between the models. The OLS model provides three parameters the slope and intercepts for the two features in line with the linear assumption.
In contrast, the regression tree chart above displays for each node of the first two levels the feature and threshold used to split the data (note that features can be used repeatedly), as well as the current value of the mean-squared error (MSE), the number of samples, and predicted value based on these training samples.
The tree chart also highlights the uneven distribution of samples across the nodes as the numbers vary between $14,700$ and $3,200$ samples after only two splits.
statsmodels OLS¶
ols_model = sm.OLS(endog=y, exog=sm.add_constant(X2)).fit()
print(ols_model.summary())
Compare with Linear Time Series Models¶
statsmodels AR(2) Model¶
The coefficients are slightly different because an AR model treats returns as a single time series instead creating groups by ticker.
ar_model = sm.tsa.ARMA(endog=y, order=(2,0)).fit()
pd.DataFrame({'AR(2)': ar_model.params.values,
'OLS': ols_model.params.values},
index=ols_model.params.index)
ar_preds = ar_model.predict()
ARMA(2,2)¶
arma_model = sm.tsa.ARMA(endog=y, order=(2, 2)).fit()
print(arma_model.summary())
arma_preds = arma_model.predict()
preds = X2.assign(arma=arma_preds, ar=ar_preds).sample(frac=.1).sort_values(['t-1', 't-2'])
preds.info()
q = 20
preds['t-1q'] = pd.qcut(preds['t-1'], q=q, labels=list(range(1, q+1))).astype(int)
preds['t-2q'] = pd.qcut(preds['t-2'], q=q, labels=list(range(1, q+1))).astype(int)
Decision Surfaces¶
The plot of the decision surface for both time series models illustrates how the ARMA model is capable of representing a more complex dynamic relationship.
fig, axes = plt.subplots(ncols=2, figsize=(13, 6))
sns.heatmap(preds.groupby(['t-1q', 't-2q']).ar.median().unstack(), ax=axes[0], cmap='BuPu_r')
axes[0].set_title('AR(2) Model')
sns.heatmap(preds.groupby(['t-1q', 't-2q']).arma.median().unstack(), ax=axes[1], cmap='BuPu_r')
axes[1].set_title('ARMA(2,2) Model')
b, t = axes[0].set_ylim()
b += 0.5
t -= 0.5
axes[0].set_ylim(b, t)
b, t = axes[1].set_ylim()
b += 0.5
t -= 0.5
axes[1].set_ylim(b, t)
fig.tight_layout();
sklearn Linear Regression¶
lin_reg = LinearRegression()
lin_reg.fit(X=X2,y=y)
lin_reg.intercept_
lin_reg.coef_
Linear Regression vs Regressin Tree Decision Surfaces¶
To further illustrate the different assumptions about the functional form of the relationships between the input variables and the output, we can visualize current return predictions as a function of the feature space, that is, as a function of the range of values for the lagged returns (features). The following figure shows the current period return as a function of returns one and two periods ago for linear regression and the regression tree:
The linear-regression model result on the left side underlines the linearity of the relationship between lagged and current returns, whereas the regression tree chart on the right illustrates the non-linear relationship encoded in the recursive partitioning of the feature space.
t1, t2 = np.meshgrid(np.linspace(X2['t-1'].quantile(.01), X2['t-1'].quantile(.99), 100),
np.linspace(X2['t-2'].quantile(.01), X2['t-2'].quantile(.99), 100))
X_data = np.c_[t1.ravel(), t2.ravel()]
fig, axes = plt.subplots(ncols=2, figsize=(13,5))
# Linear Regression
ret1 = lin_reg.predict(X_data).reshape(t1.shape)
surface1 = axes[0].contourf(t1, t2, ret1, cmap='coolwarm')
plt.colorbar(mappable=surface1, ax=axes[0])
# Regression Tree
ret2 = reg_tree_t2.predict(X_data).reshape(t1.shape)
surface2 = axes[1].contourf(t1, t2, ret2, cmap='coolwarm')
plt.colorbar(mappable=surface2, ax=axes[1])
# Format plots
titles = ['Linear Regression', 'Regression Tree']
for i, ax in enumerate(axes):
ax.set_xlabel('t-1')
ax.set_ylabel('t-2')
ax.set_title(titles[i])
fig.suptitle('Decision Surfaces', fontsize=20)
fig.tight_layout()
fig.subplots_adjust(top=.9);
Basic Classification Tree¶
A classification tree works just like the regression version, except that categorical nature of the outcome requires a different approach to making predictions and measuring the loss. While a regression tree predicts the response for an observation assigned to a leaf node using the mean outcome of the associated training samples, a classification tree instead uses the mode, that is, the most common class among the training samples in the relevant region. A classification tree can also generate probabilistic predictions based on relative class frequencies.
Loss Functions¶
When growing a classification tree, we also use recursive binary splitting but, instead of evaluating the quality of a decision rule using the reduction of the mean-squared error.
- Classification error rate: The fraction of the training samples in a given (leave) node that do not belong to the most common class.
Alternative measures:
Alternative measures are preferred because they are more sensitive to node purity than the classification error rate. Node purity refers to the extent of the quantity of a single class in a node. A node that only contains samples with outcomes belonging to a single class is pure and imply successful classification.
Gini Impurity is a measurement of the likelihood of an incorrect classification of a new instance of a random variable, if that new instance were randomly classified according to the distribution of class labels from the training subset.
- Gini impurity is lower bounded by $0$, with $0$ occurring if the data set contains only one class.
- Information Gain, or IG for short, measures the reduction in entropy or surprise by splitting a dataset according to a given value of a random variable. A larger information gain suggests a lower entropy group or groups of samples, and hence less surprise.
- Entropy quantifies how much information there is in a random variable, or more specifically its probability distribution. A skewed distribution has a low entropy, a distribution where events have equal probability will have larger entropy.
Where classification outcomes take on $K$ values, $0,1,\dots,K-1$, for a given node, $m$, that represents a region, $R_m$, of the feature space and where $p_{mk}$ is the proportion of outcomes of the $k$ class in the $m$ node:
$$ Entropy = -\sum_{k} P_{mk} log(p_{mk}) $$$$ Gini = \sum_{k} P_{mk} (1 - p_{mk}) $$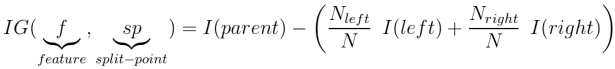
def entropy(f):
return (-f*np.log2(f) - (1-f)*np.log2(1-f))/2
def gini(f):
return 2*f*(1-f)
def misclassification_rate(f):
return np.where(f<=.5, f, 1-f)
Both the Gini Impurity and the Cross-Entropy measure take on smaller values when the class proportions approach zero or one, that is, when the child nodes become pure as a result of the split and are highest when the class proportions are even or $0.5$ in the binary case.
The chart below visualizes the values assumed by these two measures and the misclassification error rates across the $[0, 1]$ interval of proportions.
x = np.linspace(0, 1, 10000)
(pd.DataFrame({'Gini': gini(x),
'Entropy': entropy(x),
'Misclassification Rate': misclassification_rate(x)}, index=x)
.plot(title='Classification Loss Functions', lw=2, figsize=(10,6)));
Compare computation time¶
Gini is often preferred over entropy because it computes faster:
%%timeit
misclassification_rate(x)
%%timeit
gini(x)
%%timeit
entropy(x)
Configure Tree¶
clf_tree_t2 = DecisionTreeClassifier(criterion='gini',
splitter='best',
max_depth=4,
min_samples_split=2,
min_samples_leaf=1,
min_weight_fraction_leaf=0.0,
max_features=None,
random_state=804,
max_leaf_nodes=None,
min_impurity_decrease=0.0,
min_impurity_split=None,
class_weight=None,
presort=False)
Train Tree¶
clf_tree_t2.fit(X=X2, y=y_binary)
Visualize Tree¶
dot_data = export_graphviz(clf_tree_t2,
out_file=None,
feature_names=X2.columns,
class_names=['Down', 'Up'],
max_depth=2,
filled=True,
rounded=True,
special_characters=True)
# Draw graph
graph = pydotplus.graph_from_dot_data(dot_data)
# Show graph
Image(graph.create_png())
Compare with Logistic Regression¶
Statsmodels¶
model = sm.Logit(endog=y_binary, exog=sm.add_constant(X2)).fit()
print(model.summary())
sklearn¶
logistic_reg = LogisticRegression()
logistic_reg.fit(X=X2, y=y_binary)
logistic_reg.coef_
Plot Decision Surfaces¶
fig, axes = plt.subplots(ncols=2, figsize=(12,5))
# Linear Regression
ret1 = logistic_reg.predict_proba(X_data)[:, 1].reshape(t1.shape)
surface1 = axes[0].contourf(t1, t2, ret1, cmap='coolwarm')
plt.colorbar(mappable=surface1, ax=axes[0])
# Regression Tree
ret2 = clf_tree_t2.predict_proba(X_data)[:, 1].reshape(t1.shape)
surface2 = axes[1].contourf(t1, t2, ret2, cmap='coolwarm')
plt.colorbar(mappable=surface2, ax=axes[1])
# Format plots
titles = ['Logistic Regression', 'Classification Tree']
for i, ax in enumerate(axes):
ax.set_xlabel('t-1')
ax.set_ylabel('t-2')
ax.set_title(titles[i])
fig.suptitle('Decision Surfaces', fontsize=20)
fig.tight_layout()
fig.subplots_adjust(top=.9);
Regression Tree with all Features¶
We now train, visualize, and evaluate a regression tree with up to $5$ consecutive splits using $80\%$ of the samples for training to predict the remaining $20\%$.
We are taking a shortcut here to simplify the illustration and use the built-in train_test_split, which does not protect against lookahead bias, as our custom cv class iterator. The tree configuration implies up to $2^5=32$ leaf nodes that, on average in the balanced case, would contain over $4,300$ of the training samples.
Train-Test Split¶
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=804)
Configure Tree¶
The output after training the model displays all the DecisionTreeClassifier parameters that we will address in more detail in the next section when we discuss parameter-tuning.
regression_tree = DecisionTreeRegressor(criterion='mse',
splitter='best',
max_depth=5,
min_samples_split=2,
min_samples_leaf=1,
min_weight_fraction_leaf=0.0,
max_features=None,
random_state=804,
max_leaf_nodes=None,
min_impurity_decrease=0.0,
min_impurity_split=None,
presort=False)
Train Model¶
regression_tree.fit(X=X_train, y=y_train)
Visualize Tree¶
The result shows that the model uses a variety of different features and indicates the split rules for both continuous and categorical (dummy) variables.
dot_data = export_graphviz(regression_tree,
out_file=None,
feature_names=X_train.columns,
max_depth=3,
filled=True,
rounded=True,
special_characters=True)
# Draw graph
graph = pydotplus.graph_from_dot_data(dot_data)
# Show graph
Image(graph.create_png())
Evaluate Test Set¶
y_pred = regression_tree.predict(X_test)
np.sqrt(mean_squared_error(y_pred=y_pred, y_true=y_test))
Classification Tree with all Features¶
We will now train, visualize, and evaluate a classification tree with up to $5$ consecutive splits using $80\%$ of the samples for training to predict the remaining $20\%$. We are taking a shortcut here to simplify the illustration and use the built-in train_test_split, which does not protect against lookahead bias, as our custom iterator. The tree configuration implies up to $2^5=32$ leaf nodes that, on average in the balanced case, would contain over $4,300$ of the training samples.
Train-Test Split¶
X_train, X_test, y_train, y_test = train_test_split(X, y_binary, test_size=0.2, random_state=804)
clf = DecisionTreeClassifier(criterion='gini',
max_depth=5,
random_state=804)
clf.fit(X=X_train, y=y_train)
To evaluate the predictive accuracy of our first classification tree, we will use our test set to generate predicted class probabilities.
The .predict_proba() method produces one probability for each class. In the binary class, these probabilities are complementary and sum to $1$, so we only need the value for the positive class.
# only keep probabilities for pos. class
y_score = clf.predict_proba(X=X_test)[:, 1]
To evaluate the generalization error, we will use the area under the curve (AUC) based on the receiver-operating characteristic. The result indicates a significant improvement above and beyond the baseline value of $0.5$ for a random prediction:
roc_auc_score(y_score=y_score, y_true=y_test)
Plot Tree¶
dot_data = export_graphviz(clf,
out_file=None,
feature_names=X_train.columns,
class_names=['Down', 'Up'],
max_depth=3,
filled=True,
rounded=True,
special_characters=True)
# Draw graph
graph = pydotplus.graph_from_dot_data(dot_data)
# Show graph
Image(graph.create_png())
Evaluate Test Set¶
y_pred = clf.predict_proba(X_test)[:, 1]
roc_auc_score(y_true=y_test, y_score=y_pred)
Print Decision Path¶
from sklearn.tree._tree import Tree
def tree_to_code(tree, feature_names):
if isinstance(tree, DecisionTreeClassifier):
model = 'clf'
elif isinstance(tree, DecisionTreeRegressor):
model = 'reg'
else:
raise ValueError('Need Regression or Classification Tree')
tree_ = tree.tree_
feature_name = [
feature_names[i] if i != _tree.TREE_UNDEFINED else "undefined!"
for i in tree_.feature
]
print("def tree({}):".format(", ".join(feature_names)))
def recurse(node, depth):
indent = " " * depth
if tree_.feature[node] != _tree.TREE_UNDEFINED:
name = feature_name[node]
threshold = tree_.threshold[node]
print(indent, f'if {name} <= {threshold:.2%}')
recurse(tree_.children_left[node], depth + 1)
print(indent, f'else: # if {name} > {threshold:.2%}')
recurse(tree_.children_right[node], depth + 1)
else:
pred = tree_.value[node][0]
val = pred[1]/sum(pred) if model == 'clf' else pred[0]
print(indent, f'return {val:.2%}')
recurse(0, 1)
tree_to_code(clf_tree_t2, X2.columns)
Overfitting, Regularization & Parameter Tuning¶
Decision trees have a strong tendency to overfit, especially when a dataset has a large number of features relative to the number of samples. Overfitting increases the prediction error because the model does not only learn the signal contained in the training data, but also the noise.
There are several ways to address the risk of overfitting:
- Dimensionality reduction improves the feature-to-sample ratio by representing the existing features with fewer, more informative, and less noisy features.
- Ensemble models, such as random forests, combine multiple trees while randomizing the tree construction.
- Decision trees provide several regularization hyperparameters to limit the growth of a tree and the associated complexity. While every split increases the number of nodes, it also reduces the number of samples available per node to support a prediction. For each additional level, twice the number of samples is needed to populate the new nodes with the same sample density.
- Tree-pruning is an additional tool to reduce the complexity of a tree by eliminating nodes or entire parts of a tree that add little value but increase the model's variance. Cost-complexity-pruning, for instance, starts with a large tree and recursively reduces its size by replacing nodes with leaves, essentially running the tree construction in reverse. The various steps produce a sequence of trees that can then be compared using cross-validation to select the ideal size.
Decision Tree Parameters¶
The following table lists key parameters available for this purpose in the sklearn decision tree implementation. After introducing the most important parameters, we will illustrate how to use cross-validation to optimize the hyperparameter settings with respect to the bias-variance tradeoff and lower prediction errors:
| Parameter | Default | Options | Description |
|---|---|---|---|
| criterion | gini | Regression: MSE, MAE Classification: Gini impurity, Cross Entropy | Metric to evaluate split quality. |
| splitter | best | best, random | How to choose the split at each node. Supported strategies are “best” to choose the best split and “random” to choose the best random split. |
| max_depth | None | int | Max # of levels in tree. Split nodes until max_depth is reached or all leaves are pure or all leaves contain less than min_samples_split samples. |
| max_features | None | None: max_features=n_features; int; float (fraction): int(max_features * n_features) auto, sqrt: max_features=sqrt(n_features). log2: max_features=log2(n_features). | # of features to consider when evaluating split |
| max_leaf_nodes | None | None: unlimited # of leaf nodes int | Continue to split nodes that reduce relative impurity the most until reaching max_leaf_nodes. |
| min_impurity_decrease | 0 | float | Split node if impurity decreases by at least this value. |
| min_samples_leaf | 1 | int; float (as percentage of N) | Minimum # of samples to be at a leaf node. A split will only be considered if there are at least min_samples_leaf training samples in each of the left and right branches. May smoothen the model, esp. for regression. |
| min_samples_split | 2 | int; float (as percentage of N) | The minimum number of samples required to split an internal node: |
| min_weight_fraction_leaf | 0 | NA | The minimum weighted fraction of the sum total of weights (of all the input samples) required to be at a leaf node. Samples have equal weight when sample_weight is not provided (in fit method). |
| presort | False | NA | Sort the data to speed up the search for best splits during training. Can slow down training on 'large' datasets but may speed up training on small data or with small max_depth setting. |
| class_weight | None | balanced: inversely proportional to class frequencies dict: {class_label: weight} list of dicts (for multi-output) | Weights associated with classes |
- The
max_depthparameter imposes a hard limit on the number of consecutive splits and represents the most straightforward way to cap the growth of a tree.
- The
min_samples_splitandmin_samples_leafparameters are alternative, data-driven ways to limit the growth of a tree. Rather than imposing a hard limit on the number of consecutive splits, these parameters control the minimum number of samples required to further split the data. The latter guarantees a certain number of samples per leaf, while the former can create very small leaves if a split results in a very uneven distribution. Small parameter values facilitate overfitting, while a high number may prevent the tree from learning the signal in the data.
- The default values are often quite low, and you should use cross-validation to explore a range of potential values. You can also use a float to indicate a percentage as opposed to an absolute number.
def plot_cv_results(cv_scores, metric='AUC', parameter='Max. Depth'):
fig, ax = plt.subplots(figsize=(12,6))
df = pd.DataFrame(cv_scores)
sns.tsplot(df.values, time=df.columns, ax=ax, lw=2)
ax.set_xlabel(parameter)
ax.set_ylabel(metric)
ax.set_title(f'{len(df)}-Fold Cross-Validation Result \nBest {parameter} = {df.mean().idxmin()} \nBest {metric} = {round(df[df.mean().idxmin()].mean(),3)}')
if metric == 'AUC':
ax.axvline(df.mean().idxmax(), ls='--', c='k', lw=1);
ax.axhline(classification_benchmark(), c='red', lw=1, ls='--')
ax.set_title(f'{len(df)}-Fold Cross-Validation Result \nBest {parameter} = {df.mean().idxmax()} \nBest {metric} = {round(df[df.mean().idxmax()].mean(),3)}')
else:
ax.axvline(df.mean().idxmin(), ls='--', c='k', lw=1);
ax.axhline(regression_benchmark(), c='red', lw=1, ls='--')
Cross-Validation Score¶
Cross-validation is the most important tool to obtain an unbiased estimate of the generalization error, which in turn permits an informed choice among the various configuration options. sklearn offers several tools to facilitate the process of cross-validating numerous parameter settings, namely the GridSearchCV class.
cv = OneStepTimeSeriesSplit(n_splits=10)
clf_results = {}
for max_depth in range(1, 26):
clf_tree = DecisionTreeClassifier(criterion='gini',
max_depth=max_depth,
min_samples_leaf=5,
random_state=804)
clf_results[max_depth] = cross_val_score(clf_tree,
X=X,
y=y_binary,
scoring='roc_auc',
n_jobs=4,
cv=cv)
plot_cv_results(clf_results)
Train-Test Result¶
max_depths = range(1, 26)
How to inspect the tree structure¶
The following code illustrates how to run cross-validation more manually to obtain custom tree attributes, such as the total number of nodes or leaf nodes associated with certain hyperparameter settings.
The following function accesses the internal .tree_ attribute to retrieve information about the total node count, and how many of these nodes are leaf nodes:
def get_leaves_count(tree):
t = tree.tree_
n = t.node_count
leaves = len([i for i in range(t.node_count) if t.children_left[i]== -1])
return leaves
We can combine this information with the train and test scores to gain detailed knowledge about the model behavior throughout the cross-validation process, as follows:
train_scores, val_scores, leaves = {}, {}, {}
for max_depth in max_depths:
print(max_depth, end=' ', flush=True)
clf = DecisionTreeClassifier(criterion='gini',
max_depth=max_depth,
min_samples_leaf=500,
max_features='auto',
random_state=804)
train_scores[max_depth], val_scores[max_depth], leaves[max_depth] = [], [], []
for train_idx, test_idx in cv.split(X):
X_train, y_train, = X.iloc[train_idx], y_binary.iloc[train_idx]
X_test, y_test = X.iloc[test_idx], y_binary.iloc[test_idx]
clf.fit(X=X_train, y=y_train)
train_pred = clf.predict_proba(X=X_train)[:, 1]
train_score = roc_auc_score(y_score=train_pred, y_true=y_train)
train_scores[max_depth].append(train_score)
test_pred = clf.predict_proba(X=X_test)[:, 1]
val_score = roc_auc_score(y_score=test_pred, y_true=y_test)
val_scores[max_depth].append(val_score)
leaves[max_depth].append(get_leaves_count(clf))
clf_train_scores = pd.DataFrame(train_scores)
clf_valid_scores = pd.DataFrame(val_scores)
clf_leaves = pd.DataFrame(leaves)
Regression Tree¶
Cross-Validation Scores¶
reg_results = {}
for max_depth in range(1, 26):
reg_tree = DecisionTreeRegressor(criterion='mse',
max_depth=max_depth,
min_samples_leaf=500,
random_state=804)
reg_results[max_depth] = np.sqrt(-cross_val_score(reg_tree,
X=X,
y=y,
scoring='neg_mean_squared_error',
n_jobs=4,
cv=cv))
plot_cv_results(reg_results, metric='RMSE')
train_scores, val_scores, leaves = {}, {}, {}
for max_depth in max_depths:
print(max_depth, end=' ', flush=True)
reg_tree = DecisionTreeRegressor(max_depth=max_depth,
min_samples_leaf=500,
max_features= 'sqrt',
random_state=804)
train_scores[max_depth], val_scores[max_depth], leaves[max_depth] = [], [], []
for train_idx, test_idx in cv.split(X):
X_train, y_train, = X.iloc[train_idx], y.iloc[train_idx]
X_test, y_test = X.iloc[test_idx], y.iloc[test_idx]
reg_tree.fit(X=X_train, y=y_train)
train_pred = reg_tree.predict(X=X_train)
train_score = np.sqrt(mean_squared_error(
y_pred=train_pred, y_true=y_train))
train_scores[max_depth].append(train_score)
test_pred = reg_tree.predict(X=X_test)
val_score = np.sqrt(mean_squared_error(
y_pred=test_pred, y_true=y_test))
val_scores[max_depth].append(val_score)
leaves[max_depth].append(get_leaves_count(reg_tree))
reg_train_scores = pd.DataFrame(train_scores)
reg_valid_scores = pd.DataFrame(val_scores)
reg_leaves = pd.DataFrame(leaves)
Plot Results¶
fig, axes = plt.subplots(ncols=2, figsize=(13, 5))
time = pd.Series(max_depths, name='Max. Depth')
sns.tsplot(data=np.dstack((reg_train_scores, reg_valid_scores)),
time=time,
condition=['Train', 'Valid'],
ci=95,
ax=axes[0],
lw=2)
ax0 = axes[0].twinx()
sns.tsplot(data=reg_leaves.values, time=time, ax=ax0, ls=':', lw=1, color='k')
ax0.set_yscale('log', basey=2)
ax0.grid(None)
ax0.set_ylabel('# Leaf Nodes')
axes[0].set_title(f'Regression Tree \nBest Max Depth = {reg_valid_scores.mean().idxmin()} \nBest valid RMSE = {round(reg_valid_scores[reg_valid_scores.mean().idxmin()].mean(),3)}', fontsize=14)
axes[0].set_ylabel('RMSE')
axes[0].yaxis.set_major_formatter(
FuncFormatter(lambda y, _: '{:.2%}'.format(y)))
axes[0].axvline(x=reg_valid_scores.mean().idxmin(), ls='--', c='r', lw=1)
axes[0].axhline(y=regression_benchmark(), ls='-', c='k', lw=1)
sns.tsplot(data=np.dstack((clf_train_scores, clf_valid_scores)),
time=pd.Series(max_depths, name='Max. Depth'),
condition=['Train', 'Valid'],
ci=95,
ax=axes[1],
lw=2)
ax1 = axes[1].twinx()
sns.tsplot(data=clf_leaves.values, time=time, ax=ax1, ls=':', lw=1, color='k')
ax1.set_yscale('log', basey=2)
ax1.grid(None)
axes[1].set_title(f'Classification Tree \nBest Max Depth = {clf_valid_scores.mean().idxmax()} \nBest valid AUC = {round(clf_valid_scores[clf_valid_scores.mean().idxmax()].mean(),3)}', fontsize=14)
axes[1].set_ylabel('ROC AUC')
axes[1].axvline(x=clf_valid_scores.mean().idxmax(), ls='--', c='r', lw=1)
axes[1].axhline(y=classification_benchmark(), ls='-', c='k', lw=1)
fig.suptitle(f'Train-Validation Scores', fontsize=24)
fig.tight_layout()
fig.subplots_adjust(top=.8)
GridSearch¶
sklearn provides a method to define ranges of values for multiple hyperparameters. It automates the process of cross-validating the various combinations of these parameter values to identify the optimal configuration. Let's walk through the process of automatically tuning our model.
Classification Tree¶
The first step is to instantiate a model object and define a dictionary where the keywords name the hyperparameters, and the values list the parameter settings to be tested:
clf = DecisionTreeClassifier(random_state=804)
param_grid = {'max_depth': range(10, 20),
'min_samples_leaf': [250, 500, 750],
'max_features': ['sqrt', 'auto']
}
Then, instantiate the GridSearchCV object, providing the estimator object and parameter grid, as well as a scoring method and cross-validation choice to the initialization method. We'll use an object of our custom OneStepTimeSeriesSplit class, initialized to use ten folds for the cv parameter, and set the scoring to the roc_auc metric. We can parallelize the search using the n_jobs parameter and automatically obtain a trained model that uses the optimal hyperparameters by setting refit=True.
gridsearch_clf = GridSearchCV(estimator=clf,
param_grid=param_grid,
scoring='roc_auc',
n_jobs=4,
cv=cv,
refit=True,
return_train_score=True)
With all settings in place, we can fit GridSearchCV just like any other model:
gridsearch_clf.fit(X=X, y=y_binary)
The training process produces some new attributes for our GridSearchCV object, most importantly the information about the optimal settings and the best cross-validation score (now using the proper setup that avoids lookahead bias).
Setting max_depth to 16, min_samples_leaf to 750, and randomly selecting only a number corresponding to the square root of the total number of features when deciding on a split, produces the best results, with an AUC of 0.529:
gridsearch_clf.best_params_
gridsearch_clf.best_score_
Regression Tree¶
reg_tree = DecisionTreeRegressor(random_state=804)
param_grid = {'max_depth': [1,2],
'min_samples_leaf': [10],
'max_features': [None, 'sqrt']
}
gridsearch_reg = GridSearchCV(estimator=reg_tree,
param_grid=param_grid,
scoring='neg_mean_squared_error',
n_jobs=4,
cv=cv,
refit=True,
return_train_score=True)
gridsearch_reg.fit(X=X, y=y)
gridsearch_reg.best_params_
np.sqrt(-gridsearch_reg.best_score_)
regression_benchmark()
Learning Curves¶
A learning curve is a useful tool that displays how the validation and training score evolve as the number of training samples evolves.
The purpose of the learning curve is to find out whether and how much the model would benefit from using more data during training. It is also useful to diagnose whether the model's generalization error is more likely driven by bias or variance.
If, for example, both the validation score and the training score converge to a similarly low value despite an increasing training set size, the error is more likely due to bias, and additional training data is unlikely to help.
Classifier¶
sizes = np.arange(.1, 1.01, .1)
train_sizes, train_scores, valid_scores = learning_curve(gridsearch_clf.best_estimator_,
X,
y_binary,
train_sizes=sizes,
cv=cv,
scoring='roc_auc',
n_jobs=4,
shuffle=True,
random_state=804)
clf_data = np.dstack((train_scores.T, valid_scores.T))
fig, axes = plt.subplots(ncols=2, figsize=(14, 5))
condition = ['Training', 'Validation']
sns.tsplot(data=np.dstack((clf_train_scores, clf_valid_scores)),
time=pd.Series(max_depths, name='Max. Depth'),
condition=condition,
ci=95,
ax=axes[0],
lw=2)
ax1 = axes[0].twinx()
sns.tsplot(data=clf_leaves.values, time=time, ax=ax1, ls=':', lw=1, color='k')
ax1.set_yscale('log', basey=2)
ax1.grid(None)
axes[0].set_title(f'Classification Tree \nBest Max Depth = {clf_valid_scores.mean().idxmax()} \nBest valid AUC = {round(clf_valid_scores[clf_valid_scores.mean().idxmax()].mean(),3)}', fontsize=14)
axes[0].set_ylabel('ROC AUC')
axes[0].axvline(x=clf_valid_scores.mean().idxmax(), ls='--', c='r', lw=1)
axes[0].axhline(y=classification_benchmark(), ls='-', c='k', lw=1)
sns.tsplot(data=clf_data,
time=pd.Series(train_sizes, name='Train Size'),
condition=condition,
ci=95,
ax=axes[1],
lw=2)
axes[1].set_title('Learning Curve')
axes[1].set_ylabel('ROC AUC')
axes[1].xaxis.set_major_formatter(FuncFormatter(lambda x, _: '{:,.0f}'.format(x)))
fig.tight_layout();
Regression Tree¶
train_sizes, train_scores, valid_scores = learning_curve(gridsearch_reg.best_estimator_,
X, y,
train_sizes=sizes,
cv=cv,
scoring='neg_mean_squared_error',
n_jobs=4,
shuffle=True,
random_state=804)
reg_data = np.dstack((train_scores.T, valid_scores.T))
Plot Result¶
time = pd.Series(train_sizes, name='Train Size')
fig, axes = plt.subplots(ncols=2, figsize=(13,5))
sns.tsplot(data=clf_data,
time=time,
condition=['Train', 'Valid'],
ci=95,
ax=axes[0],
lw=2)
axes[0].set_title('Best Classification Tree')
axes[0].set_ylabel('ROC AUC')
axes[0].xaxis.set_major_formatter(FuncFormatter(lambda x, _: '{:,.0f}'.format(x)))
sns.tsplot(data=np.sqrt(-reg_data),
time=time,
condition=['Train', 'Valid'],
ci=95,
ax=axes[1],
lw=2)
axes[1].set_title('Best Regression Tree')
axes[1].set_ylabel('RMSE')
axes[1].yaxis.set_major_formatter(FuncFormatter(lambda y, _: '{:.2%}'.format(y)))
axes[1].xaxis.set_major_formatter(FuncFormatter(lambda x, _: '{:,.0f}'.format(x)))
fig.suptitle('Learning Curves', fontsize=24)
fig.tight_layout()
fig.subplots_adjust(top=.85);
Feature Importance¶
Decision trees can not only be visualized to inspect the decision path for a given feature, but also provide a summary measure of the contribution of each feature to the model fit to the training data.
The feature importance captures how much the splits produced by the feature helped to optimize the model's metric used to evaluate the split quality, which in our case is the Gini Impurity index.
A feature's importance is computed as the (normalized) total reduction of this metric and takes into account the number of samples affected by a split. Hence, features used earlier in the tree where the nodes tend to contain more samples typically are considered of higher importance.
top_n = 15
labels = X.columns.str.replace('_', ' ').str.capitalize()
fi_clf = (pd.Series(gridsearch_clf.best_estimator_.feature_importances_,
index=labels).sort_values(ascending=False).iloc[:top_n])
fi_reg = (pd.Series(gridsearch_reg.best_estimator_.feature_importances_,
index=labels).sort_values(ascending=False).iloc[:top_n])
fig, axes= plt.subplots(ncols=2, figsize=(12,6))
color = cm.rainbow(np.linspace(.4,.9, top_n))
fi_clf.sort_values().plot.barh(ax=axes[0], title='Classification Tree', color=color)
fi_reg.sort_values().plot.barh(ax=axes[1], title='Regression Tree', color=color)
fig.suptitle(f'Top {top_n} Feature Importances', fontsize=18)
fig.tight_layout()
fig.subplots_adjust(top=.85);
fig, axes = plt.subplots(ncols=2, figsize=(13,5))
(pd.DataFrame({'Gini': gini(x),
'Entropy': entropy(x),
'Misclassification Rate': misclassification_rate(x)}, index=x)
.plot(title='Classification Loss Functions', lw=2, ax=axes[0], ylim=(0, .55)))
top_n = 15
labels = X.columns.str.replace('_', ' ').str.capitalize()
fi_clf = (pd.Series(gridsearch_clf.best_estimator_.feature_importances_,
index=labels).sort_values(ascending=False).iloc[:top_n])
color = cm.rainbow(np.linspace(.4,.9, top_n))
fi_clf.sort_values().plot.barh(ax=axes[1], title='Feature Importances', color=color)
fig.tight_layout()
Strengths and weaknesses of decision trees¶
Regression and classification trees take a very different approach to prediction when compared to the linear models we have explored so far. How do you decide which model is more suitable to the problem at hand? Consider the following:
- If the relationship between the outcome and the features is approximately linear (or can be transformed accordingly), then linear regression will likely outperform a more complex method, such as a decision tree that does not exploit this linear structure.
- If the relationship appears highly non-linear and more complex, decision trees will likely outperform the classical models.
Several advantages have made decision trees very popular:¶
- They are fairly straightforward to understand and to interpret, not least because they can be easily visualized and are thus more accessible to a non-technical audience. Decision trees are also referred to as white-box models given the high degree of transparency about how they arrive at a prediction. Black-box models, such as ensembles and neural networks may deliver better prediction accuracy but the decision logic is often much more challenging to understand and interpret.
- Decision trees require less data preparation than models that make stronger assumptions about the data or are more sensitive to outliers and require data standardization (such as regularized regression).
- Some decision tree implementations handle categorical input, do not require the creation of dummy variables (improving memory efficiency), and can work with missing values, but this is not the case for
sklearn.
- Prediction is fast because it is logarithmic in the number of leaf nodes (unless the tree becomes extremely unbalanced).
- It is possible to validate the model using statistical tests and account for its reliability.
Decision trees also have several key disadvantages:¶
- Decision trees have a built-in tendency to overfit to the training set and produce a high generalization error. Key steps to address this weakness are pruning (not yet supported by
sklearn) as well as regularization using the various early-stopping criteria outlined in the previous sections.
- Closely related is the high variance of decision trees that results from their ability to closely adapt to a training set so that minor variations in the data can produce wide swings in the structure of the decision trees and, consequently, the predictions the model generates. The key mechanism to address the high variance of decision trees is the use of an ensemble of randomized decision trees that have low bias and produce uncorrelated prediction errors.
- The greedy approach to decision-tree learning optimizes based on local criteria, that is, to reduce the prediction error at the current node and does not guarantee a globally optimal outcome. Again, ensembles consisting of randomized trees help to mitigate this problem.
- Decision trees are also sensitive to unbalanced class weights and may produce biased trees. One option is to oversample the underrepresented or under-sample the more frequent class. It is typically better, though, to use class weights and directly adjust the objective function.