Comparing Linear and Nonlinear Correlations

  • Comparing Maximal Information Coefficient to Pearson, Spearman, Cosine Similarity, Distance Correlation, Mutual Information on bivariate data.

Objectives

The code below will include the following:

  • simulating linear and nonlinear data and relationships with and without noise
  • Comparing performance of MIC, Pearson, Spearman, Distance Correlation, Mutual Information and Cosine similarity
  • Visualising the results

Correlation and dependence

  • Correlation or dependence is any statistical relationship, whether causal or not, between two random variables or bivariate data. In the broadest sense correlation is any statistical association, though it commonly refers to the degree to which a pair of variables are linearly related. Correlations are useful because they can indicate a predictive relationship that can be exploited in practice.

Imports

In [1]:
import warnings
import itertools
import matplotlib.pyplot as plt
import matplotlib.cm as cm
import seaborn as sns
import numpy as np
import pandas as pd
import scipy
from scipy import stats
import statsmodels.api as sm
from sklearn.feature_selection import f_regression, mutual_info_regression
from minepy import MINE
In [2]:
sns.set(style="whitegrid", color_codes=True)
warnings.filterwarnings('ignore')
In [3]:
# Set random number generator seed for reproducibility
np.random.seed(220)

Generate Linear and Nonlinear bivariate data

In [4]:
"""generate linear relationship"""
x_l = np.linspace(0,10,100) 
y_l0 = 2.0+0.7*x_l

noise_l = np.random.randn(100) 
y_l1 = 2.+0.7*x_l+noise_l

"""generate exponential linear relationship"""
x_e = np.linspace(0,10,100) 
y_e0 = np.exp((x_e+2) ** 0.5)*x_l

noise_e = np.random.uniform(0.01,250, 100)
y_e1 = y_e0+noise_e

"""generate quadriatic relationship"""
x_q = np.linspace(-10,10,100) 
y_q0 = 2.0+0.7*x_q**2 + 0.5*x_q

noise_q = np.random.uniform(0.5,15, 100) 
y_q1 = 2.+ 0.7*x_q**2+ 0.5*x_q + noise_q

"""generate sinusoidal relationship"""
x_s = np.linspace(-3,2,100) 
#y_s0 = 3.0+np.sin(x_s)
y_s0 = np.exp(-(x_s+2) ** 2) + np.cos((x_s-2)**2)
noise_s = np.random.uniform(0.5,5, 100) 
#y_s1 = 2.+ np.sin(x_s) + noise_s
y_s1 = np.exp(-(x_s+2) ** 2) + np.cos((x_s-2)**2) + noise_s

"""generate circular relationship"""
angle = np.linspace(0,10,100) 
r = 50 + np.random.normal(0, 8, angle.shape)
x_cn = r * np.cos(angle)
y_cn = r * np.sin(angle)
idx = np.random.permutation(angle.shape[0])
x_cn = x_cn[idx]
y_cn = y_cn[idx]
angle = np.arctan2(x_cn, y_cn)
order = np.argsort(angle)
x_cn = x_cn[order]
y_cn = y_cn[order]

x_c = np.cos(angle)
y_c = np.sin(angle)
idx = np.random.permutation(angle.shape[0])
x_c = x_c[idx]
y_c = y_c[idx]
angle = np.arctan2(x_c, y_c)
order = np.argsort(angle)
x_c = x_c[order]
y_c = y_c[order]

Plot bivariate data

In [5]:
fig, ax = plt.subplots(nrows=5, ncols=2, figsize=(13,13))

ax[0,0].plot(x_s, y_s0, color='r')
ax[0,1].plot(x_s, y_s1, color='r')

ax[1,0].plot(x_q, y_q0, color='b')
ax[1,1].plot(x_q, y_q1, color='b')
    
ax[2,0].plot(x_l, y_l0, color='g')
ax[2,1].plot(x_l, y_l1, color='g')

ax[3,0].plot(x_e, y_e0, color='purple')
ax[3,1].plot(x_e, y_e1, color='purple')

ax[4,0].plot(x_c, y_c, color='y')
ax[4,1].plot(x_cn, y_cn, color='y')

ax[0,0].set_title('Sinusoidal')
ax[0,1].set_title('Sinusoida + Noisel')
ax[1,0].set_title('Quadriatic')
ax[1,1].set_title('Quadriatic + Noisel')
ax[2,0].set_title('Linear')
ax[2,1].set_title('Linear + Noisel')
ax[3,0].set_title('Exp Linear')
ax[3,1].set_title('Exp Linear + Noisel')
ax[4,0].set_title('Circular')
ax[4,1].set_title('Circular + Noisel')

plt.tight_layout();

Create a dictionary of $x$ and $y$ values for each of the generated bivariate datasets.

In [6]:
ts_dict = {'lin':      {'x': x_l, 'y': y_l0}, 
           'lin_n':    {'x': x_l, 'y': y_l1},
           'exp lin':  {'x': x_e, 'y': y_e0}, 
           'exp lin_n':{'x': x_e, 'y': y_e1},
           'quadr':    {'x': x_q, 'y': y_q0}, 
           'quadr_n':  {'x': x_q, 'y': y_q1},
           'sin':      {'x': x_l, 'y': y_s0}, 
           'sin_n':    {'x': x_l, 'y': y_s1},
           'cir':      {'x': x_c,  'y': y_c}, 
           'cir_n':    {'x': x_cn, 'y': y_cn}}

Function to create a dataframe of resulting $x$ and $y$ data correlations from a dictionary of the generated bivariate datasets.

In [7]:
def compare_corrs(Dict=ts_dict):
    
    mine = MINE(alpha=0.6, c=15, est='mic_approx')
    dist_corrs, sprearman_corrs, pearson_corrs, mi_reg, f_tests, cos_sims, mic_s = [], [], [], [], [], [], []
    
    for ts in Dict.keys():
    
        X = ts_dict[ts]['x']
        y = ts_dict[ts]['y']

        dist_corr = scipy.spatial.distance.correlation(X,y)
        sprearman_corr, s_p_val = stats.spearmanr(X,y)
        pearson_corr, p_p_val = stats.pearsonr(X,y)
        cos_dist = scipy.spatial.distance.cosine(X,y)
    
        mi = mutual_info_regression(X.reshape(-1,1), y.reshape(-1,1))
        f_test, _ = f_regression(X.reshape(-1,1), y.reshape(-1,1))
    
        mine.compute_score(X,y)
        mic =  mine.mic() 
    
        dist_corrs.append(dist_corr)
        sprearman_corrs.append(sprearman_corr)
        pearson_corrs.append(pearson_corr)
        cos_sims.append(1-cos_dist)
        mi_reg.append(mi[0])
        f_tests.append(f_test[0])
        mic_s.append(mic)
    
    corrs_df = pd.DataFrame(dist_corrs, index=ts_dict.keys(), columns=['Dist_corr'])
    corrs_df['cos_sim'] = cos_sims
    #corrs_df['f_reg'] = f_tests / np.max(f_tests)
    corrs_df['mutual_info'] = mi_reg / np.max(mi_reg)
    corrs_df['spear_corr'] = sprearman_corrs
    corrs_df['pear_corr'] = pearson_corrs
    corrs_df['mic'] = mic_s

    return corrs_df

I subtracted the cosine distance from $1$, because it a distance metric. The farther the distance more dissimilar, inversely the smaller the distance the more correlated are two variables.

Linear and Nonlinear Correlations

Distance correlation

  • Distance correlation or distance covariance is a measure of dependence between two paired random vectors of arbitrary, not necessarily equal, dimension. The population distance correlation coefficient is zero if the random vectors are independent. Thus, distance correlation measures both linear and nonlinear association between two random variables or random vectors.
  • Instead of assessing how two variables tend to co-vary in their distance from their respective means, distance correlation assesses how they tend to co-vary in terms of their distances from all other points.
  • The distance correlation of two random variables is obtained by dividing their distance covariance by the product of their distance standard deviations. The distance correlation is
$$ \operatorname {dCor} (X,Y)={\frac {\operatorname {dCov} (X,Y)}{\sqrt {\operatorname {dVar} (X)\,\operatorname {dVar} (Y)}}}, $$
  • Correlation distance goes from $0$ - $2$, with $0$ being PERFECT correlation, $1$ being no correlation, and $2$ being PERFECT NEGATIVE CORRELATION. So a small correlation distance value means close together in THE correlation space. A high correlation = high relationship; LOW CORRELATION DISTANCE = high relationship.

Cosine Similarity

Alt text that describes the graphic

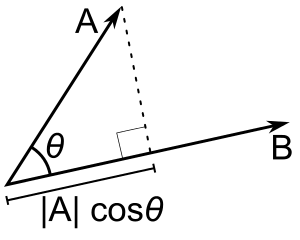
  • Cosine similarity​ is a metric often used to measure how similar the documents are irrespective of their size. Mathematically, it measures the cosine of the angle between two vectors projected in a multi-dimensional space. The cosine similarity is advantageous because even if the two similar documents are far apart by the Euclidean distance (due to the size of the document), chances are they may still be oriented closer together. The smaller the angle, higher the cosine similarity.
  • Uses the angle between $2$ lines
  • When the angle is $0$ (the vectors point in the exact same direction), $cos(\theta)$ will equal $1$.
  • When the angle is $-180°$, (the vectors point in exact opposite directions), then $cos(\theta)$ will equal $-1$.
  • When the angle is $90°$ (the vectors point in completely unrelated directions), then $cos(\theta)$ will equal $0$.
  • Given two vectors of attributes, $A$ and $B$, the cosine similarity, $\cos{\theta}$:
$$ \vec{a} \cdot \vec{b} = \|\vec{a}\|\|\vec{b}\|\cos{\theta} \\ \\ \cos{\theta} = \frac{\vec{a} \cdot \vec{b}}{\|\vec{a}\|\|\vec{b}\|} $$

Mutual Information

  • The mutual information (MI) between a feature and the outcome is a measure of the mutual dependence between the two variables. It is given the name ,information gain, when applied to variable selection. It extends the notion of correlation to nonlinear relationships. More specifically, it quantifies the information obtained about one random variable through the other random variable. MI determines how different the joint distribution of the pair ($X$,$Y$) is to the product of the marginal distributions of $X$ and $Y$.
  • Let $(X,Y)$ be a pair of random variables with values over the space ${\mathcal{X}} \times {\mathcal{Y}}$. If their joint distribution is $P_{(X,Y)}$ and the marginal distributions are $P_{X}$ and $P_{Y}$, the mutual information is defined as
$$ I(X;Y)=D_{\mathrm {KL} }(P_{(X,Y)}\|P_{X}\otimes P_{Y})$$
  • Information Gain, or IG for short, measures the reduction in entropy or surprise by splitting a dataset according to a given value of a random variable. A larger information gain suggests a lower entropy group or groups of samples, and hence less surprise.
  • Entropy quantifies how much information there is in a random variable, or more specifically its probability distribution. A skewed distribution has a low entropy, a distribution where events have equal probability will have larger entropy.

In a binary case:

  • Entropy is $0$ if all samples belong to the same class for a node (i.e., pure)
  • Entropy is $1$ samples contain both classes for a node (i.e., $50\%$ for each class awful)
  • Skewed Probability Distribution (unsurprising): Low entropy.
  • Balanced Probability Distribution (surprising): High entropy.

Pearson correlation

  • The Pearson correlation coefficient is a statistic that measures linear correlation between two variables $X$ and $Y$. It has a value between $+1$ and $−1$. A value of $+1$ is total positive linear correlation, $0$ is no linear correlation, and $−1$ is total negative linear correlation.
  • Pearson's correlation coefficient when applied to a population is commonly represented by the Greek letter ρ (rho) and may be referred to as the population correlation coefficient or the population Pearson correlation coefficient. Given a pair of random variables $(X,Y)$, the formula for $p$ is:
$$\rho _{X,Y}={\frac {\operatorname {cov} (X,Y)}{\sigma _{X}\sigma _{Y}}}$$

where:

  • $\operatorname{cov}$ is the covariance
  • $\sigma _{X}$ is the standard deviation of $X$
  • $\sigma_Y$ is the standard deviation of $Y$

Spearman's rank correlation

  • Spearman's rank correlation coefficient is a nonparametric measure of rank correlation (statistical dependence between the rankings of two variables). It assesses how well the relationship between two variables can be described using a monotonic function.
  • A monotonic function (or monotone function) is a function between ordered sets that preserves or reverses the given order. A is called monotonic if and only if it is either entirely non-increasing, or entirely non-decreasing.
  • The Spearman correlation between two variables is equal to the Pearson correlation between the rank values of those two variables; while Pearson's correlation assesses linear relationships, Spearman's correlation assesses monotonic relationships (whether linear or not). If there are no repeated data values, a perfect Spearman correlation of $+1$ or $−1$ occurs when each of the variables is a perfect monotone function of the other.

Maximal information Coefficient

  • The maximal information coefficient (MIC) (Simon and Tibshirani, $2011$) is an information theory-based measure of association that can capture a wide range of functional and non-functional relationships between variables.
  • Formally, MIC is equal to the coefficient of determination (R2). MIC takes values between $0$ and $1$, where $0$ means statistical independence and $1$ means a completely noiseless relationship.
$$ \operatorname{MIC}(X,Y) = \operatorname{max}\{I(x,y) \: \: / \: \operatorname{log}_2 \operatorname{min}\{n_x, n_y\}\} $$
  • From the formula we can see that MIC($X$,$Y$) is the mutual information between random variables $X$ and $Y$ normalized by their minimum joint entropy. I interpret the MIC as the percent of a variable $Y$ that can be explained by a variable $X$. In addition to generalizing well over a range of relationships, another useful property of MIC is its equitability. This means that MIC assigns the same score to equally noisy relationships, regardless of the type of relationship. This is good because a lot of times we do not know the distribution of our data or the nature of relationships between variables.
  • Able to capture wide range of linear and non-linear relationships (cubic, exponential, sinusoidal, superposition of functions)
  • Does not make any assumptions about the distribution of the variables.
  • Robust to outliers because of its mutual information foundation.
  • Does not report the direction or the type of relationship.
  • Low statistical power: when Simon and Tibshirani compared the performance of MIC with Pearson’s and distance correlation on simulated independent data, they reported that in most cases MIC had less power.

Heatmap of resulting correlations

In [8]:
corrs_df = compare_corrs(Dict=ts_dict)

plt.figure(figsize=(12,5))
sns.heatmap(corrs_df, annot=True)
b, t = plt.ylim() 
b += 0.5 
t -= 0.5 
plt.ylim(b, t) 
plt.yticks(rotation=0)
plt.show()

Barplot of each generated bivariate $x$ and $y$ data correlations to compare different measures correlation.

In [9]:
tmp_fts = corrs_df.T

fig, axs = plt.subplots(ncols=2, nrows=0, figsize=(25, 35))
plt.subplots_adjust(right=2.5)
plt.subplots_adjust(top=2)

cm = plt.get_cmap('jet')
colors = np.linspace(0.1, 1, len(tmp_fts))

for i, feature in enumerate(list(tmp_fts), 1):
        
    plt.subplot(len(list(tmp_fts.columns)), 2, i)
    
    sns.barplot(tmp_fts[feature], tmp_fts[feature].index)
    plt.title(f'{feature}', fontsize=28, fontweight='bold') 
    plt.xlabel('')
    
    for j in range(2):
        plt.tick_params(axis='x', labelsize=25)
        plt.tick_params(axis='y', labelsize=25)

plt.tight_layout()
plt.show()

Results

Linear:

  • Expectedly, all the metrics performed well on the noiseless data. However, Cosine similarity was more robust to the added noise.
  • Winner: Cosine Similarity

Exponential Linear:

  • Expectedly, all the metrics performed well on the noiseless data. However, Cosine similarity was more robust to the added noise.
  • Winner: Cosine Similarity

Quadratic:

  • MIC greatly outperformed all the other metrics on detecting this non-linear relationship. Also note how robust MIC was when noise was added.
  • Winner: MIC

Sinusoidal:

  • MIC performed well on detecting the non-linear relationships, but the cosine similarity score was the most resistant to noise, based on the scores before and after.
  • Winner: Cosine Similarity

Circular:

  • MIC greatly outperformed all the other metrics on detecting this non-linear relationship. Also MIC​ proved to be fairly robust when noise was added.
  • Winner: MIC
In [ ]: