Basic Linear Modeling in Python¶
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
Data¶
times = [0.0,1.0,2.0,3.0,4.0,5.0,6.0]
distances = [0.00,44.05,107.16,148.44,196.40,254.44,300.00]
Reasons for Modeling: Interpolation¶
One common use of modeling is interpolation to determine a value "inside" or "in between" the measured data points. Here we will make a prediction for the value of the dependent variable distances for a given independent variable times that falls "in between" two measurements from a road trip, where the distances are those traveled for the given elapse times.
Plot Data¶
plt.scatter(times, distances)
plt.plot(times, np.poly1d(np.polyfit(times, distances, 1))(times), color='r')
plt.grid(True)
plt.xlabel('X Data Time Driven (hours)')
plt.ylabel('Y Data Distance Traveled (miles)');
# Compute the total change in distance and change in time
total_distance = distances[-1] - distances[0]
total_time = times[-1] - times[0]
# Estimate the slope of the data from the ratio of the changes
average_speed = total_distance / total_time
# Predict the distance traveled for a time not measured
elapse_time = 2.5
distance_traveled = average_speed * elapse_time
print(f"Total Distance {total_distance}")
print(f"\nTotal Time {total_time}")
print(f"\nAverage Speed {average_speed}")
print(f"\nThe distance traveled is {distance_traveled}")
Notice that the answer distance is 'inside' that range of data values, so, less than the max(distances) but greater than the min(distances)
Reasons for Modeling: Extrapolation¶
Another common use of modeling is extrapolation to estimate data values "outside" or "beyond" the range (min and max values of time) of the measured data. Here, we have measured distances for times $0$ through $5$ hours, but we are interested in estimating how far we'd go in $8$ hours. Using the same data set from the previous exercise, we have prepared a linear model distance = model(time). Use that model() to make a prediction about the distance traveled for a time much larger than the other times in the measurements.
# Plot the observed data
plt.scatter(times, distances)
# Fit a model and predict future dates
predict_vals = [0.0,1.0,2.0,3.0,4.0,5.0,6.0,8.0,9.0,10.0]
model = np.polyfit(times, distances, 1)
predicted = np.polyval(model, predict_vals)
# Plot the model
plt.plot(predict_vals, predicted, color='r')
plt.grid(True)
plt.xlabel('X Data Time Driven (hours)')
plt.ylabel('Y Data Distance Traveled (miles)');
def model(time, a0=0, a1=average_speed):
"""
Purpose:
For a given value of time, compute the model value for distance
Args:
time (float, np.ndarray): elapse time in units of hours
a0 (float): default=0, coefficient for the Zeroth order term in the model, i.e. a0 + a1*x
a1 (float): default=50, coefficient for the 1st order term in the model, i.e. a0 + a1*x
Returns:
distance (float, np.ndarray): model values corresponding to input time array, with the same length/size.
"""
distance = a0 + (a1*time)
return distance
# Select a time not measured.
time = 8
# Use the model to compute a predicted distance for that time.
distance = model(time)
# Inspect the value of the predicted distance traveled.
print(distance)
# Determine if you will make it without refueling.
answer = (distance <= 400)
print(answer)
Notice that the car can travel just to the range limit of $400$ miles, so you'd run out of gas just as you completed the trip
Reasons for Modeling: Estimating Relationships¶
Another common application of modeling is to compare two data sets by building models for each, and then comparing the models. Here, we are given data for a road trip two cars took together. The cars stopped for gas every $50$ miles, but each car did not need to fill up the same amount, because the cars do not have the same fuel efficiency (MPG). The function efficiency_model(miles, gallons) is created to estimate efficiency as average miles traveled per gallons of fuel consumed.
Data¶
car1 = {'miles': [1. , 50.9, 100.8, 150.7, 200.6, 250.5, 300.4, 350.3, 400.2, 450.1,500.],
'gallons': [0.03333333, 1.69666667, 3.36, 5.02333333, 6.68666667, 8.35, 10.01333333, 11.67666667,
13.34, 15.00333333, 16.66666667]}
car2 = {'miles': [1. , 50.9, 100.8, 150.7, 200.6, 250.5, 300.4, 350.3, 400.2, 450.1, 500. ],
'gallons': [0.02 , 1.018, 2.016, 3.014, 4.012, 5.01, 6.008, 7.006, 8.004, 9.002, 10. ]}
Plot Data¶
plt.scatter(car1['miles'], car1['gallons'], label='car1')
plt.scatter(car2['miles'], car2['gallons'], label='car2')
plt.grid(True)
plt.ylabel('Y Data Fuel Consumed (gallons)')
plt.xlabel('X Data Distance Traveled (miles)')
plt.legend();
# Complete the function to model the efficiency.
def efficiency_model(miles, gallons):
return np.mean(miles/gallons)
# Use the function to estimate the efficiency for each car.
car1['mpg'] = efficiency_model(np.array(car1['miles']), np.array(car1['gallons']))
car2['mpg'] = efficiency_model(np.array(car2['miles']), np.array(car2['gallons']))
# Finish the logic statement to compare the car efficiencies.
if car1['mpg'] > car2['mpg'] :
print('car1 is the best')
elif car1['mpg'] < car2['mpg'] :
print('car2 is the best')
else:
print('the cars have the same efficiency')
Notice the original plot that visualized the raw data, the slope is $1$/MPG and so car1 is steeper than car2, but if you plot(gallons, miles) the slope is MPG, and so car2 has a steeper slope than car1
plt.scatter(car1['gallons'], car1['miles'], label='car1')
plt.scatter(car2['gallons'], car2['miles'], label='car2')
plt.grid(True)
plt.xlabel('Y Data Fuel Consumed (gallons)')
plt.ylabel('X Data Distance Traveled (miles)')
plt.legend();
Mean, Deviation, & Standard Deviation¶
The mean describes the center of the data. The standard deviation describes the spread of the data. But to compare two variables, it is convenient to normalize both. Here, we are provided with two arrays of data, which are highly correlated, and we will compute and visualize the normalized deviations of each array.
Create Data¶
num_samples = 50
# The desired mean values of the sample.
mu = [6.01327144, 301.09351247]
# The desired covariance matrix.
cov = [[1.44408412e+00, 7.11018554e+01],
[7.11018554e+01, 3.62713035e+03]]
# Generate the random samples.
Y = np.random.multivariate_normal(mu, cov, size=num_samples)
# x and y data
x = Y[:,0]
y = Y[:,1]
# Compute the deviations by subtracting the mean offset
dx = x - np.mean(x)
dy = y - np.mean(y)
# Normalize the data by dividing the deviations by the standard deviation
zx = dx / np.std(x)
zy = dy / np.std(y)
plt.figure(figsize=(10,1))
plt.plot(dx, color='r')
plt.plot(dy, color='b')
plt.xlabel('Array Index')
plt.ylabel('Deviations of x & y')
plt.show()
plt.figure(figsize=(10,1))
plt.plot(zx, color='r')
plt.plot(zy, color='b')
plt.xlabel('Array Index')
plt.ylabel('Normalized Deviations of x & y')
plt.show()
Notice how hard it is to compare $dx$ and $dy$, versus comparing the normalized $zx$ and $zy$.
Covariance vs Correlation¶
Covariance is a measure of whether two variables change ("vary") together. It is calculated by computing the products, point-by-point, of the deviations seen in the previous exercise, dx[n]*dy[n], and then finding the average of all those products.
Correlation is in essence the normalized covariance. Here, we have with two arrays of data, which are highly correlated, and we will visualize and compute both the covariance and the correlation.
# Compute the covariance from the deviations.
dx = x - np.mean(x)
dy = y - np.mean(y)
covariance = np.mean(dx * dy)
print("Covariance: ", covariance)
# Compute the correlation from the normalized deviations.
zx = dx / np.std(x)
zy = dy / np.std(y)
correlation = np.mean(zx * zy)
print("Correlation: ", correlation)
plt.plot(zx*zy)
plt.axhline(0, linestyle='dashed', color='r')
plt.xlabel('Array Index')
plt.ylabel('Product of Normalized Deviations')
plt.title(f'Correlation = np.mean(zx*zy) = {round(correlation,2)*100}');
Notice that we've plotted the product of the normalized deviations, and labeled the plot with the correlation, a single value that is the mean of that product. The product is always positive and the mean is typical of how the two vary together.
Correlation Strength¶
Intuitively, we can look at the plots provided and "see" whether the two variables seem to "vary together".
- Data Set A: $x$ and $y$ change together and appear to have a strong relationship.
- Data Set B: there is a rough upward trend; $x$ and $y$ appear only loosely related.
- Data Set C: looks like random scatter; $x$ an $y$ do not appear to change together and are unrelated.
Create Data¶
# Generate correlated random variables
# The desired number of samples
num_samples = 50
# The desired mean values of the sample.
mu = [4.71815762, 9.44076045, 5.09321393, 10.16904155, 5.0165893, 10.6883259]
# The desired covariance matrix.
cov = [[1.36208968, 2.70163528, 1.37835545, 2.78133499, 1.73359544, 0.95056748],
[2.70163528, 5.40596017, 2.73195338, 5.65673871, 3.43406231, 2.30481703],
[1.37835545, 2.73195338, 1.47904869, 3.23872554, 1.77708497, 1.88996037],
[2.78133499, 5.65673871, 3.23872554, 24.2142715, 3.65117281, 14.5615414],
[1.73359544, 3.43406231, 1.77708497, 3.65117281, 2.25638144, 2.41304719],
[0.95056748, 2.30481703, 1.88996037, 14.5615414, 2.41304719, 295.880271]]
# Generate the random samples.
y = np.random.multivariate_normal(mu, cov, size=num_samples)
# Create a dictionaty from the random samples split into 3 sets each with an x and y array of values
data_sets = {'A': {'x':y[:,0],
'y':y[:,1]},
'B': {'x':y[:,2],
'y':y[:,3]},
'C': {'x':y[:,4],
'y':y[:,5]}}
Recall that deviations differ from the mean, and we normalized by dividing the deviations by standard deviation. Here we will compare the $3$ data sets by computing correlation, and determining which data set has the most strongly correlated variables $x$ and $y$.
for name, data in data_sets.items():
plt.scatter(data['x'], data['y'], color='k')
plt.axhline(0, linestyle='dashed', color='b')
plt.grid(True)
plt.xlabel('X')
plt.ylabel('Y')
plt.title(f'Data set {name} has correlation = ?')
plt.show()
# Complete the function that will compute correlation.
def correlation(x,y):
x_dev = x - np.mean(x)
y_dev = y - np.mean(y)
x_norm = x_dev / np.std(x)
y_norm = y_dev / np.std(y)
return np.mean(x_norm * y_norm)
# Compute and store the correlation for each data set in the list.
for name, data in data_sets.items():
data['correlation'] = correlation(data['x'], data['y'])
print('\ndata set {} has correlation {:.2f}'.format(name, data['correlation']))
# Assign the data set with the best correlation.
best_data = data_sets['A']
Note that the strongest relationship is in Dataset $A$, with correlation closest to $1.0$ and the weakest is Datatset $C$ with correlation value closest to zero.
Taylor Series¶
The Taylor series of a function is an infinite sum of terms, where each term has a larger exponent like x, x2, x3, etc. A Taylor Series is expressed in terms of the function's derivatives at a single point. For most common functions, the function and the sum of its Taylor series are equal near this point. Taylor's series are named after Brook Taylor who introduced them in $1715$.
- approximate any curve
- polynomial form
- often, first order is enough
- The derivative of a function of a real variable measures the sensitivity to change of the function value (output value) with respect to a change in its argument (input value). Derivatives are a fundamental tool of calculus. For example, the derivative of the position of a moving object with respect to time is the object's velocity: this measures how quickly the position of the object changes when time advances.
- A polynomial in a single indeterminate $x$ can always be written (or rewritten) in the form
- where $a_{0},\ldots ,a_{n}$ are constants and $x$ is the indeterminate. The word "indeterminate" means that $x$ represents no particular value, although any value may be substituted for it. The mapping that associates the result of this substitution to the substituted value is a function, called a polynomial function.
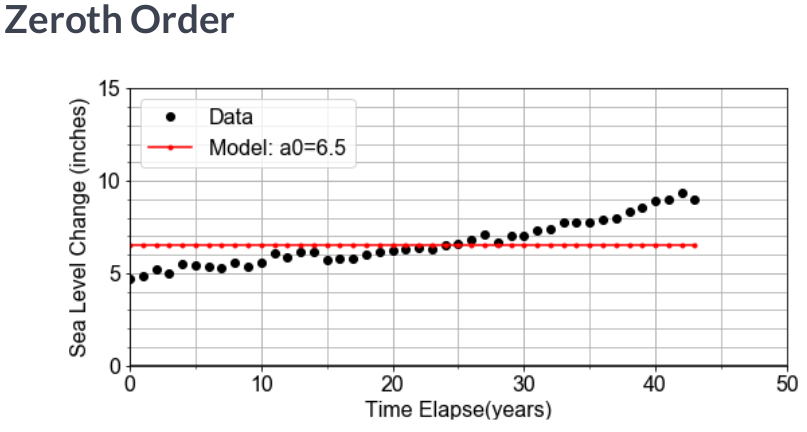
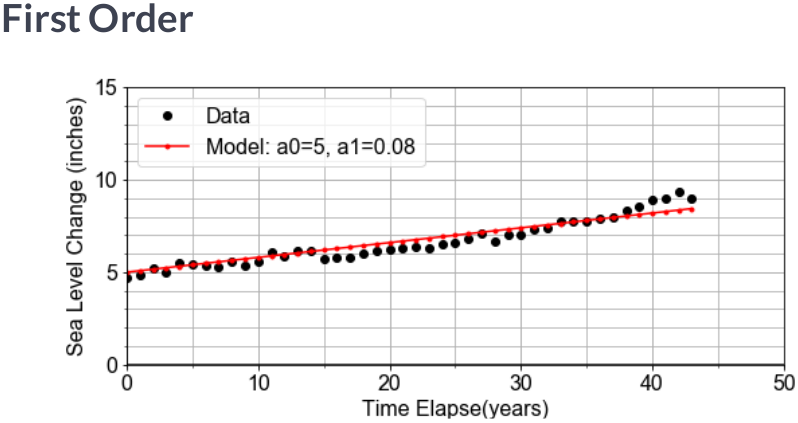
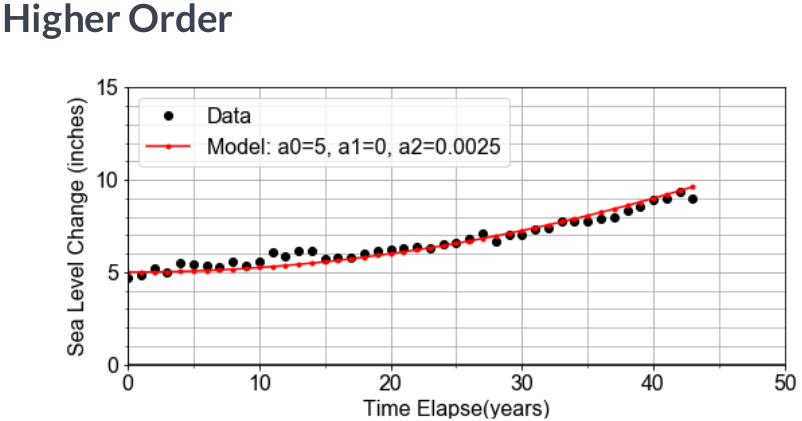
Model Components¶
Previously, we have been given a pre-defined model to work with. In this Here, we will implement a model function that returns model values for $y$, computed from input $x$ data, and any input coefficients for the "zero-th" order term a0, the "first-order" term a1, and a quadratic term a2 of a model.
Recall that "first order" is linear, so we'll set the defaults for this general linear model with a2=0, but later, we will change this for comparison.
# Define the general model as a function
def model(x, a0=3, a1=2, a2=0):
return a0 + (a1*x) + (a2*x*x)
# Generate array x, then predict y values for specific, non-default a0 and a1
x = np.linspace(-10, 10, 21)
y = model(x)
plt.scatter(x, y)
plt.plot(x, np.poly1d(np.polyfit(x, y, 1))(x), color='r')
plt.grid(True)
plt.title('Plot of modeled Y for given data X')
plt.xlabel('X')
plt.ylabel('Y');
Notice that we used model() to compute predicted values of y for given possibly measured values of x. The model takes the independent data and uses it to generate a model for the dependent variables corresponding values.
Model Parameters¶
Now that we've built a general model, let's "optimize" or "fit" it to a new measured data set, xd, yd, by finding the specific values for model parameters a0, a1 for which the model data and the measured data line up on a plot.
This is an iterative visualization strategy, where we start with a guess for model parameters, pass them into the model(), over-plot the resulting modeled data on the measured data, and visually check that the line passes through the points. If it doesn't, we change the model parameters and try again.
Load Data¶
df_xy = pd.read_csv('df_xy.csv').drop('Unnamed: 0', axis=1)
df_xy.info()
xd = df_xy['X'].values
yd = df_xy['Y'].values
Plot Data¶
plt.scatter(xd, yd)
plt.grid(True)
plt.xlim(-5,15)
plt.ylim(-250,750)
plt.axvline(0, color='k')
plt.axhline(0, color='k')
plt.title('Hiking Trip')
plt.xlabel('Step distance (km)')
plt.ylabel('Altitude (meters)');
# Complete the plotting function definition
def plot_data_with_model(xd, yd, ym):
plt.scatter(xd, yd)
plt.grid(True)
plt.xlim(-5,15)
plt.ylim(-250,750)
plt.axvline(0, color='k')
plt.axhline(0, color='k')
plt.title('Hiking Trip')
plt.xlabel('Step distance (km)')
plt.ylabel('Altitude (meters)');
plt.plot(xd, ym, color='red') # over-plot modeled y data
plt.show()
return
# Select new model parameters a0, a1, and generate modeled `ym` from them.
a0 = 150
a1 = 25
ym = model(xd, a0, a1)
# Plot the resulting model to see whether it fits the data
fig = plot_data_with_model(xd, yd, ym)
Notice again that the measured x-axis data xd is used to generate the modeled y-axis data ym so to plot the model, you are plotting ym vs xd, which may seem counter-intuitive at first. But we are modeling the $y$ response to a given $x$; we are not modeling $x$.
Linear Proportionality¶
The definition of temperature scales is related to the linear expansion of certain liquids, such as mercury and alcohol. Originally, these scales were literally rulers for measuring length of fluid in the narrow marked or "graduated" tube as a proxy for temperature. The alcohol starts in a bulb, and then expands linearly into the tube, in response to increasing temperature of the bulb or whatever surrounds it.
Here, we will explore the conversion between the Fahrenheit and Celsius temperature scales as a demonstration of interpreting slope and intercept of a linear relationship within a physical context.
# Complete the function to convert C to F
def convert_scale(temps_C):
(freeze_C, boil_C) = (0, 100)
(freeze_F, boil_F) = (32, 212)
change_in_C = boil_C - freeze_C
change_in_F = boil_F - freeze_F
slope = change_in_F / change_in_C
intercept = freeze_F - freeze_C
temps_F = intercept + (slope * temps_C)
return temps_F
# Use the convert function to compute values of F and plot them
temps_C = np.linspace(0, 100, 101)
temps_F = convert_scale(temps_C)
plt.plot(temps_C, temps_F)
plt.grid(True)
plt.ylabel('Temperature (Fahrenheit)')
plt.xlabel('Temperature (Celsius)');
Rate of Change (ROC)¶
The rate of change - ROC - is the speed at which a variable changes over a specific period of time. ROC is often used when speaking about momentum, and it can generally be expressed as a ratio between a change in one variable relative to a corresponding change in another; graphically, the rate of change is represented by the slope of a line. The ROC is often illustrated by the Greek letter delta $\Delta$.
Slope and Rates-of-Change¶
Here, we will model the motion of a car driving (roughly) constant velocity by computing the average velocity over the entire trip. The linear relationship modeled is between the time elapsed and the distance traveled.
In this case, the model parameter a1, or slope, is approximated or "estimated", as the mean velocity, or put another way, the "rate-of-change" of the distance ("rise") divided by the time ("run").
Load Data¶
df_td = pd.read_csv('time_distance.csv').drop('Unnamed: 0', axis=1)
df_td.info()
times = df_td['times']
distances = df_td['distances']
# Compute an array of velocities as the slope between each point
diff_distances = np.diff(distances)
diff_times = np.diff(times)
velocities = diff_distances / diff_times
# Chracterize the center and spread of the velocities
v_avg = np.mean(velocities)
v_max = np.max(velocities)
v_min = np.min(velocities)
v_range = v_max - v_min
plt.scatter(times[1:], velocities, label='Velocities')
plt.axhline(v_avg, color='r', lw=5, alpha=0.4, label='Mean velocity')
plt.ylim(0,100)
plt.grid(True)
plt.ylabel('Instantaneous velocity (Kilometers/Hours)')
plt.xlabel('Time (hours)')
plt.legend();
Generally we might use the average velocity as the slope in our model. But notice that there is some random variation in the instantaneous velocity values when plotted as a time series. The range of values v_max - v_min is one measure of the scale of that variation, and the standard deviation of velocity values is another measure.
Ordinary least squares¶
In statistics, ordinary least squares (OLS) is a type of linear least squares method for estimating the unknown parameters in a linear regression model. OLS chooses the parameters of a linear function of a set of explanatory variables by the principle of least squares: minimizing the sum of the squares of the differences between the observed dependent variable (values of the variable being observed) in the given dataset and those predicted by the linear function.
Simple linear regression model
If the data matrix $X$ contains only two variables, a constant and a scalar regressor $x_i$, then this is called the "simple regression model". It provides much simpler formulas even suitable for manual calculation. The parameters are commonly denoted as ($\alpha$, $\beta$):
$$y_{i}=\alpha +\beta x_{i}+\varepsilon _{i}$$The least squares estimates in this case are given by simple formulas
$${\begin{aligned}{\hat {\beta }}&={\frac {\sum {x_{i}y_{i}}-{\frac {1}{n}}\sum {x_{i}}\sum {y_{i}}}{\sum {x_{i}^{2}}-{\frac {1}{n}}(\sum {x_{i}})^{2}}}={\frac {\operatorname {Cov} [x,y]}{\operatorname {Var} [x]}}\\{\hat {\alpha }}&={\overline {y}}-{\hat {\beta }}\,{\overline {x}}\ ,\end{aligned}}$$where Var(.) and Cov(.) are sample parameters.
Intercept and Starting Points¶
Here, we will see the intercept and slope parameters in the context of modeling measurements taken of the volume of a solution contained in a large glass jug. The solution is composed of water, grains, sugars, and yeast. The total mass of both the solution and the glass container was also recorded, but the empty container mass was not noted.
Our job is to use the pandas DataFrame df, with data columns volumes and masses, to build a linear model that relates the masses (y-data) to the volumes (x-data). The slope will be an estimate of the density (change in mass / change in volume) of the solution, and the intercept will be an estimate of the empty container weight (mass when volume=$0$).
Load Data¶
fpath_csv = 'https://assets.datacamp.com/production/repositories/1480/datasets/e4c4cdd076de27d3c1bccfe1d0019d279c08d2fc/solution_data.csv'
df = pd.read_csv(fpath_csv, comment='#')
print(df.info())
print(df.head())
# Import ols from statsmodels, and fit a model to the data
from statsmodels.formula.api import ols
model_fit = ols(formula="masses ~ volumes", data=df)
model_fit = model_fit.fit()
# Extract the model parameter values, and assign them to a0, a1
a0 = model_fit.params['Intercept']
a1 = model_fit.params['volumes']
# Print model parameter values with meaningful names, and compare to summary()
print( "container_mass = {:0.4f}".format(a0) )
print( "\nsolution_density = {:0.4f}".format(a1) )
print('\n',model_fit.summary())
Residual in a Regression Model¶
A residual is the vertical distance between a data point and the regression line. Each data point has one residual. They are positive if they are above the regression line and negative if they are below the regression line. If the regression line actually passes through the point, the residual at that point is zero.
Errors and residuals¶
The error (or disturbance) of an observed value is the deviation of the observed value from the (unobservable) true value of a quantity of interest (for example, a population mean), and the residual of an observed value is the difference between the observed value and the estimated value of the quantity of interest (for example, a sample mean). The distinction is most important in regression analysis, where the concepts are sometimes called the regression errors and regression residuals
Residual Sum of Squares (RSS)¶
The residual sum of squares measures the amount of error remaining between the regression function and the data set. A smaller residual sum of squares figure represents a regression function. Residual sum of squares–also known as the sum of squared residuals–essentially determines how well a regression model explains or represents the data in the model.
$$ SS_{\text{res}}=\sum _{i}(y_{i}-f_{i})^{2}=\sum _{i}e_{i}^{2}\ $$Residual Sum of the Squares¶
Previously we saw that the altitude along a hiking trail was roughly fit by a linear model, and we introduced the concept of differences between the model and the data as a measure of model goodness.
Here, we'll work with the same measured data, and quantifying how well a model fits it by computing the sum of the square of the "differences", also called "residuals".
# Function to generate x and y data
def load_data():
num_pts=21; a0=3.0*50; a1=0.5*50; mu=0; sigma=1; ae=0.5*50; seed=1234;
np.random.seed(seed)
xmin = 0
xmax = 10
x1 = np.linspace(xmin, xmax, num_pts)
e1 = np.array([np.random.normal(mu, sigma) for n in range(num_pts)])
y1 = a0 + (a1*x1) + ae*e1
return x1, y1
# Load the data
x_data, y_data = load_data()
# Model the data with specified values for parameters a0, a1
y_model = model(x_data, a0=150, a1=25)
# Compute the RSS value for this parameterization of the model
rss = np.sum(np.square(y_data - y_model))
print(f"RSS = {rss}")
The value we compute for RSS is not meaningful by itself, but later it becomes meaningful in context when we compare it to other values of RSS computed for other parameterizations of the model.
Minimizing the Residuals¶
Here, we will complete a function to visually compare model and data, and compute and print the RSS. We will call it more than once to see how RSS changes when you change values for a0 and a1. We'll see that the values for the parameters we found earlier are the ones needed to minimize the RSS.
# Complete function to load data, build model, compute RSS, and plot
def compute_rss_and_plot_fit(a0, a1):
xd, yd = load_data()
ym = model(xd, a0, a1)
residuals = ym - yd
rss = np.sum(np.square(residuals))
summary = "Parameters a0={}, a1={} yield RSS={:0.2f}".format(a0, a1, rss)
plt.scatter(xd, yd)
plt.grid(True)
plt.xlim(-5,15)
plt.ylim(-250,750)
plt.axvline(0, color='k')
plt.axhline(0, color='k')
plt.title(summary)
plt.xlabel('Step distance (km)')
plt.ylabel('Altitude (meters)')
plt.plot(xd, ym, color='red') # over-plot modeled y data
plt.show()
return rss, summary
# Chose model parameter values and pass them into RSS function
rss, summary = compute_rss_and_plot_fit(a0=150, a1=25)
print(summary)
As stated earlier, the significance of RSS is in context of other values. More specifically, the minimum RSS is of value in identifying the specific set of parameter values for our model which yield the smallest residuals in an overall sense.
Visualizing the RSS Minima¶
Here we will compute and visualize how RSS varies for different values of model parameters. Start by holding the intercept constant, but vary the slope: and for each slope value, we'll compute the model values, and the resulting RSS. Once you have an array of RSS values, we will determine minimal RSS value, in code, and from that minimum, determine the slope that resulted in that minimal RSS.
Data¶
x_data = df_xy['X'].values
y_data = df_xy['Y'].values
# Function to compute RSS
def compute_rss(yd, ym):
rss = np.sum(np.square(yd-ym))
return rss
# Empty list for RSS array
rss_list = []
# Loop over all trial values in a1_array, computing rss for each
a1_array = np.linspace(15, 35, 101)
for a1_trial in a1_array:
y_model = model(x_data, a0=150, a1=a1_trial)
rss_value = compute_rss(y_data, y_model)
rss_list.append(rss_value)
# Find the minimum RSS and the a1 value from whence it came
rss_array = np.array(rss_list)
best_rss = np.min(rss_array)
best_a1 = a1_array[np.where(rss_array==best_rss)]
print('The minimum RSS = {}, came from a1 = {}'.format(best_rss, best_a1[0]))
# Plot your rss and a1 values to confirm answer
plt.scatter(a1_array, rss_array)
plt.scatter(best_a1, best_rss, color='r', s=150)
plt.grid(True)
plt.title(f'Minimum RSS = {best_rss}\n came from a1 = {best_a1[0]}')
plt.xlabel('Slope a1')
plt.ylabel('RSS');
The best slope is the one out of an array of slopes than yielded the minimum RSS value out of an array of RSS values. Python tip: notice that we started with rss_list to make it easy to .append() but then later converted tonumpy.array() to gain access to all the numpy methods.
Least-Squares with numpy¶
The formulae below are the result of working through the calculus. Here, we'll trust that the calculus correct, and implement these formulae in code using numpy.
Data¶
x = df_xy['X'].values
y = df_xy['Y'].values
# prepare the means and deviations of the two variables
x_mean = np.mean(x)
y_mean = np.mean(y)
x_dev = x - x_mean
y_dev = y - y_mean
# Complete least-squares formulae to find the optimal a0, a1
a1 = np.sum(x_dev * y_dev) / np.sum( np.square(x_dev) )
a0 = y_mean - (a1 * x_mean)
# Use the those optimal model parameters a0, a1 to build a model
y_model = model(np.array(x), a0, a1)
# plot to verify that the resulting y_model best fits the data y
fig, rss = compute_rss_and_plot_fit(a0, a1)
Notice that the optimal slope a1, according to least-squares, is a ratio of the covariance to the variance. Also, note that the values of the parameters obtained here are NOT exactly the ones used to generate the pre-loaded data (a1=$25$ and a0=$150$), but they are close to those. Least-squares does not guarantee zero error; there is no perfect solution, but in this case, least-squares is the best we can do.
Optimization with Scipy¶
It is possible to write a numpy implementation of the analytic solution to find the minimal RSS value. But for more complex models, finding analytic formulae is not possible, and so we turn to other methods.
Here we will use scipy.optimize to employ a more general approach to solve the same optimization problem.
In so doing, we will see additional return values from the method that tell answer us "how good is best". Here we will use the same measured data and parameters as seen in the last exercise for ease of comparison of the new scipy approach.
from scipy import optimize
# Define a model function needed as input to scipy
def model_func(x, a0, a1):
return a0 + (a1*x)
# Load the measured data you want to model
x_data, y_data = load_data()
# call curve_fit, passing in the model function and data; then unpack the results
param_opt, param_cov = optimize.curve_fit(model_func, x_data, y_data)
a0 = param_opt[0] # a0 is the intercept in y = a0 + a1*x
a1 = param_opt[1] # a1 is the slope in y = a0 + a1*x
# test that these parameters result in a model that fits the data
fig, rss = compute_rss_and_plot_fit(a0, a1)
Notice that we passed the function object itself, model_func into curve_fit, rather than passing in the model data. The model function object was the input, because the optimization wants to know what form in general it's solve for; had we passed in a model_func with more terms like an a2*x**2 term, we would have seen different results for the parameters output.
Least-Squares with statsmodels¶
Several python libraries provide convenient abstracted interfaces so that you need not always be so explicit in handling the machinery of optimization of the model.
As an example, in this exercise, we will use the statsmodels library in a more high-level, generalized work-flow for building a model using least-squares optimization (minimization of RSS).
x_data, y_data = load_data()
df = pd.DataFrame(dict(x_column=x_data, y_column=y_data))
# Pass data and `formula` into ols(), use and `.fit()` the model to the data
model_fit = ols(formula="y_column ~ x_column", data=df).fit()
# Use .predict(df) to get y_model values, then over-plot y_data with y_model
y_model = model_fit.predict(df)
# Extract the a0, a1 values from model_fit.params
a0 = model_fit.params['Intercept']
a1 = model_fit.params['x_column']
# Visually verify that these parameters a0, a1 give the minimum RSS
fig, rss = compute_rss_and_plot_fit(a0, a1)
Note that the params container always uses 'Intercept' for the a0 key, but all higher order terms will have keys that match the column name from the pandas DataFrame that we passed into ols().
Linear Model in Anthropology¶
If you found part of a skeleton, from an adult human that lived thousands of years ago, how could you estimate the height of the person that it came from? This exercise is in part inspired by the work of forensic anthropologist Mildred Trotter, who built a regression model for the calculation of stature estimates from human "long bones" or femurs that is commonly used today.
In this exercise, we'll use data from many living people, and the python library scikit-learn, to build a linear model relating the length of the femur (thigh bone) to the "stature" (overall height) of the person. Then, we'll apply our model to make a prediction about the height of an ancient ancestor.
Load Data¶
fpath_csv = 'https://assets.datacamp.com/production/repositories/1480/datasets/a1871736d7829e85ec4ead2212d621df69bb3977/femur_data.csv'
df = pd.read_csv(fpath_csv)
df.info()
legs = df['length'].values
heights = df['height'].values
Plot¶
plt.scatter(df['length'], df['height'])
plt.grid(True)
plt.xlim(-10,100)
plt.ylim(-30,300)
plt.axvline(0, color='k')
plt.axhline(0, color='k')
plt.title('Relating long bone length and hieght')
plt.xlabel('Femur Length (cm)')
plt.ylabel('Height (cm)');
# import the sklearn class LinearRegression and initialize the model
from sklearn.linear_model import LinearRegression
model = LinearRegression(fit_intercept=False)
# Prepare the measured data arrays and fit the model to them
legs = legs.reshape(len(legs),1)
heights = heights.reshape(len(heights),1)
model.fit(legs, heights)
# Use the fitted model to make a prediction for the found femur
fossil_leg = [[50.7]]
fossil_height = model.predict(fossil_leg)
print("Predicted fossil height = {:0.2f} cm".format(fossil_height[0,0]))
Notice that we used the pre-loaded data to fit or "train" the model, and then applied that model to make a prediction about newly collected data that was not part of the data used to fit the model. Also notice that model.predict() returns the answer as an array of shape = (1,1), so we had to index into it with the [0,0] syntax when printing.
Linear Model in Oceanography¶
Time-series data provides a context in which the "slope" of the linear model represents a "rate-of-change".
In this exercise, we will use measurements of sea level change from $1970$ to $2010$, build a linear model of that changing sea level and use it to make a prediction about the future sea level rise.
Load Data¶
fpath_csv = 'https://assets.datacamp.com/production/repositories/1480/datasets/0c1231fa1e777d3d7dd2d0ab877158a0dd219a5b/sea_level_data.csv'
df0 = pd.read_csv(fpath_csv, comment='#')
df0.info()
years = df0['year'].values
levels = df0['sea_level_inches'].values
Plot¶
plt.scatter(df0['year'], df0['sea_level_inches'])
plt.grid(True)
plt.title('Global Average Seal Level Change')
plt.xlabel('Seal Level Change (inches)')
plt.ylabel('Time (years)');
# Prepare the measured data arrays and fit the model to them
years = years.reshape(len(years),1)
levels = levels.reshape(len(years),1)
# Build a model, fit to the data
model = LinearRegression(fit_intercept=True)
model.fit(years, levels)
# Use model to make a prediction for one year, 2100
future_year = 2100
future_level = model.predict([[future_year]])
print("Prediction: year = {}, level = {:.02f}".format(future_year, future_level[0,0]))
# Use model to predict for many years, and over-plot with measured data
years_forecast = np.linspace(1970, 2100, 131).reshape(-1, 1)
levels_forecast = model.predict(years_forecast)
plt.scatter(df0['year'], df0['sea_level_inches'])
plt.plot(years_forecast, levels_forecast, color='r')
plt.grid(True)
plt.title('Global Average Seal Level Change')
plt.xlabel('Seal Level Change (inches)')
plt.ylabel('Time (years)');
Notice also that although our model is linear, the actual data appears to have an up-turn that might be better modeled by adding a quadratic or even exponential term to our model. The linear model forecast may be underestimating the rate of increase in sea level.
Linear Model in Cosmology¶
Less than $100$ years ago, the universe appeared to be composed of a single static galaxy, containing perhaps a million stars. Today we have observations of hundreds of billions of galaxies, each with hundreds of billions of stars, all moving.
The beginnings of the modern physical science of cosmology came with the publication in 1929 by Edwin Hubble that included use of a linear model.
In this exercise, we will build a model whose slope will give Hubble's Constant, which describes the velocity of galaxies as a linear function of distance from Earth.
Load Data¶
fpath_csv = 'https://assets.datacamp.com/production/repositories/1480/datasets/fffe3864d24c1864a5df0f0985a11d07bc1cd526/hubble_data.csv'
df = pd.read_csv(fpath_csv, comment='#')
df.info()
Plot¶
plt.scatter(df['distances'], df['velocities'])
plt.grid(True)
plt.xlim(-1.00,4.00)
plt.ylim(-400,1200)
plt.xlabel('Distances')
plt.ylabel('Velocities');
# Fit the model, based on the form of the formula
model_fit = ols(formula="velocities ~ distances", data=df).fit()
# Extract the model parameters and associated "errors" or uncertainties
a0 = model_fit.params['Intercept']
a1 = model_fit.params['distances']
e0 = model_fit.bse['Intercept']
e1 = model_fit.bse['distances']
# Print the results
print('For slope a1={:.02f}, the uncertainty in a1 is {:.02f}'.format(a1, e1))
print('For intercept a0={:.02f}, the uncertainty in a0 is {:.02f}'.format(a0, e0))
Interpolation: Inbetween Times¶
In this exercise, we will build a linear model by fitting monthly time-series data for the Dow Jones Industrial Average (DJIA) and then use that model to make predictions for daily data (in effect, an interpolation). Then we will compare that daily prediction to the real daily DJIA data.
A few notes on the data. "OHLC" stands for "Open-High-Low-Close", which is usually daily data, for example the opening and closing prices, and the highest and lowest prices, for a stock in a given day. DayCount is an integer number of days from start of the data collection.
Load Data¶
from pandas_datareader import data as web
import warnings
warnings.filterwarnings('ignore')
start = pd.Timestamp('2013')
end = pd.Timestamp('2015-01-01')
df_daily = web.DataReader('DJIA', 'yahoo', start, end)[['Close']]
# Resample to monthly
df_monthly = df_daily.resample('M').last()
# Count number of days elapsed since a certain date
basedate_d = df_daily.index[0]
df_daily['DayCount'] = df_daily.apply(lambda x: (x.name - basedate_d).days, axis=1)
basedate_m = df_monthly.index[0]
df_monthly['DayCount'] = df_monthly.apply(lambda x: (x.name - basedate_m).days, axis=1)
print(df_daily.head())
print('\n',df_monthly.head())
Plot Data¶
plt.figure(figsize=(10,5))
plt.scatter(df_monthly.index, df_monthly['Close'], label='Mpnthly Data')
plt.grid(True)
plt.xlabel('Date')
plt.ylabel('DJIA Close ($)')
plt.legend();
# fit a model to the df_monthly data
model_fit = ols('Close ~ DayCount', data=df_monthly).fit()
# Use the model to make a predictions for both monthly and daily data
df_monthly['Model'] = model_fit.predict(df_monthly.DayCount)
df_daily['Model'] = model_fit.predict(df_daily.DayCount)
# Calculate the RSS
rss_d = compute_rss(df_daily['Close'], df_daily['Model'])
rss_m = compute_rss(df_monthly['Close'], df_monthly['Model'])
plt.figure(figsize=(10,5))
plt.scatter(df_monthly.index, df_monthly['Close'], label='Mpnthly Data')
plt.plot(df_monthly.index, df_monthly['Model'], label='Model', color='r')
plt.grid(True)
plt.title(f'RSS {rss_m}')
plt.xlabel('Date')
plt.ylabel('DJIA Close ($)')
plt.legend();
plt.figure(figsize=(10,5))
plt.scatter(df_daily.index, df_daily['Close'], label='Daily Data')
plt.plot(df_daily.index, df_daily['Model'], label='Model', color='r')
plt.grid(True)
plt.title(f'RSS {rss_d}')
plt.xlabel('Date')
plt.ylabel('DJIA Close ($)')
plt.legend();
Notice the monthly data looked linear, but the daily data clearly has additional, nonlinear trends. Under-sampled data often misses real-world features in the data on smaller time or spatial scales. Using the model from the under-sampled data to make interpolations to the daily data can result is large residuals. Notice that the RSS value for the daily plot is more than 30 times worse than the monthly plot.
Extrapolation: Going Over the Edge¶
In this exercise, we consider the perils of extrapolation. Shown here is the profile of a hiking trail on a mountain. One portion of the trail, marked in black, looks linear, and was used to build a model. But we see that the best fit line, shown in red, does not fit outside the original "domain", as it extends into this new outside data, marked in blue.
If we want use the model to make predictions for the altitude, but still be accurate to within some tolerance, what are the smallest and largest values of independent variable x that we can allow ourselves to apply the model to?"
df = pd.read_csv('hiking.csv').drop('Unnamed: 0', axis=1)
df.info()
x_data = df['x_data'].values
y_data = df['y_data'].values
y_model = df['y_model'].values
Plot Data¶
col = np.where(np.array(x_data)<=0,'k', np.where(np.array(x_data)<10,'b','k'))
plt.scatter(x_data, y_data, c=col)
plt.plot(x_data, y_model, color='r')
plt.grid(True)
plt.xlim(-15,25)
plt.ylim(-250,750)
plt.axvline(0, color='k')
plt.axhline(0, color='k')
plt.title('Hiking Trip')
plt.xlabel('Step distance (kilometers)')
plt.ylabel('Altitude (meters)');
# Compute the residuals, "data - model", and determine where [residuals < tolerance]
residuals = np.abs(y_data - y_model)
tolerance = 100
x_good = x_data[residuals < tolerance]
# Find the min and max of the "good" values, and plot y_data, y_model, and the tolerance range
print(f'Minimum good x value = {np.min(x_good)}')
print(f'Maximum good x value = {np.max(x_good)}')
col = np.where(np.array(x_data)<=0,'k', np.where(np.array(x_data)<10,'b','k'))
plt.scatter(x_data, y_data, c=col)
plt.plot(x_data, y_model, color='r')
a = x_data <= 13
b = x_data >= -6
mask = (a & b)
plt.fill_between(x_data, y_model-tolerance, y_model+tolerance, where=mask, alpha=0.2, color='g')
plt.grid(True)
plt.xlim(-15,25)
plt.ylim(-250,750)
plt.axvline(0, color='k')
plt.axhline(0, color='k')
plt.title('Hiking Trip')
plt.xlabel('Step distance (kilometers)')
plt.ylabel('Altitude (meters)');
3 Different R's¶
Building Models:¶
- RSS:
- Used to help find the optimal values for model parameters
- The total sum of squares (proportional to the variance of the data):
- The sum of squares of residuals, also called the residual sum of squares:
Evaluating Models:¶
- RMSE:
- Root Mean Square Error (RMSE) is the standard deviation of the residuals (prediction errors). Residuals are a measure of how far from the regression line data points are; RMSE is a measure of how spread out these residuals are. In other words, it tells you how concentrated the data is around the line of best fit.
- The RMSE of an estimator $\hat{\theta}$ with respect to an estimated parameter $\theta$ is defined as the square root of the mean square error:
- The RMSE of predicted values $\hat y_t$ for times $t$ of a regression's dependent variable $y_{t}$ with variables observed over $T$ times, is computed for $T$ different predictions as the square root of the mean of the squares of the deviations:
- R-squared
- R-squared or the coefficient of determination is a statistical measure that represents the proportion of the variance for a dependent variable that's explained by an independent variable or variables in a regression model. Whereas correlation explains the strength of the relationship between an independent and dependent variable, R-squared explains to what extent the variance of one variable explains the variance of the second variable.
- The most general definition of the coefficient of determination is
RMSE Step-by-step¶
In this exercise, we will quantify the over-all model "goodness-of-fit" of a pre-built model, by computing one of the most common quantitative measures of model quality, the RMSE, step-by-step.
Data¶
x_data = df_xy['X'].values
y_data = df_xy['Y'].values
def model_fit_and_predict(x, y):
a0=150
a1=25
ym = a0 + (a1*x)
return ym
# Build the model and compute the residuals "model - data"
y_model = model_fit_and_predict(np.array(x_data), np.array(y_data))
residuals = y_model - y_data
# Compute the RSS, MSE, and RMSE and print the results
RSS = np.sum(np.square(residuals))
MSE = RSS/len(residuals)
RMSE = np.sqrt(MSE)
print('RMSE = {:0.2f}, MSE = {:0.2f}, RSS = {:0.2f}'.format(RMSE, MSE, RSS))
R-Squared¶
In this exercise we'll compute another measure of goodness, R-squared. R-squared is the ratio of the variance of the residuals divided by the variance of the data we are modeling, and in so doing, is a measure of how much of the variance in your data is "explained" by your model, as expressed in the spread of the residuals.
# Compute the residuals and the deviations
residuals = y_model - y_data
deviations = np.mean(y_data) - y_data
# Compute the variance of the residuals and deviations
var_residuals = np.mean(np.square(residuals))
var_deviations = np.mean(np.square(deviations))
# Compute r_squared as 1 - the ratio of RSS/Variance
r_squared = 1 - (var_residuals / var_deviations)
print('R-squared is {:0.2f}'.format(r_squared))
Standard error¶
The standard error (SE) of a statistic (usually an estimate of a parameter) is the standard deviation of its sampling distribution or an estimate of that standard deviation. If the parameter or the statistic is the mean, it is called the standard error of the mean (SEM).
- The standard error(SE) is very similar to standard deviation. Both are measures of spread. To put it simply, the two terms are essentially equal — but there is one important difference. While the standard error uses statistics (sample data) standard deviations use parameters (population data).
- A statistic and a parameter are very similar. They are both descriptions of groups, like $50\%$ of dog owners prefer $X$ Brand dog food. The difference between a statistic and a parameter is that statistics describe a sample. A parameter describes an entire population.
Variation Around the Trend¶
The data need not be perfectly linear, and there may be some random variation or "spread" in the measurements, and that does translate into variation of the model parameters. This variation is in the parameter is quantified by "standard error", and interpreted as "uncertainty" in the estimate of the model parameter.
In this exercise, we will use ols from statsmodels to build a model and extract the standard error for each parameter of that model.
# Store data in a DataFrame, and use ols() to fit a model to it.
df = pd.DataFrame(dict(times=times, distances=distances))
model_fit = ols(formula="distances ~ times", data=df).fit()
# Extact the model parameters and their uncertainties
a0 = model_fit.params['Intercept']
e0 = model_fit.bse['Intercept']
a1 = model_fit.params['times']
e1 = model_fit.bse['times']
# Print the results with more meaningful names
print('Estimate of the intercept = {:0.2f}'.format(a0))
print('Uncertainty of the intercept = {:0.2f}'.format(e0))
print('Estimate of the slope = {:0.2f}'.format(a1))
print('Uncertainty of the slope = {:0.2f}'.format(e1))
The size of the parameters standard error only makes sense in comparison to the parameter value itself. In fact the units are the same! So a1 and e1 both have units of velocity (meters/second), and a0 and e0 both have units of distance (meters).
Variation in Two Parts¶
Given two data sets of distance-versus-time data, one with very small velocity and one with large velocity. Notice that both may have the same standard error of slope, but different R-squared for the model overall, depending on the size of the slope ("effect size") as compared to the standard error ("uncertainty").
If we plot both data sets as scatter plots on the same axes, the contrast is clear. Variation due to the slope is different than variation due to the random scatter about the trend line. In this exercise, our goal is to compute the standard error and R-squared for two data sets and compare.
Load Data¶
df = pd.read_csv('trip2.csv').drop('Unnamed: 0', axis=1)
df.info()
Plot Data¶
plt.scatter(df['times'], df['distances1'], c='k')
plt.scatter(df['times'], df['distances2'], c='r')
plt.grid(True)
plt.title('Driving Trip')
plt.xlabel('Travel Distance (kilometers)')
plt.ylabel('Elapse Time (hours)');
# Build and fit two models, for columns distances1 and distances2 in df
model_1 = ols(formula="distances1 ~ times", data=df).fit()
model_2 = ols(formula="distances2 ~ times", data=df).fit()
# Extract R-squared for each model, and the standard error for each slope
se_1 = model_1.bse['times']
se_2 = model_2.bse['times']
rsquared_1 = model_1.rsquared
rsquared_2 = model_2.rsquared
# Print the results
print('Model 1: SE = {:0.3f}, R-squared = {:0.3f}'.format(se_1, rsquared_1))
print('Model 2: SE = {:0.3f}, R-squared = {:0.3f}'.format(se_2, rsquared_2))
Notice that the standard error is the same for both models, but the r-squared changes. The uncertainty in the estimates of the model parameters is independent from R-squared because that uncertainty is being driven not by the linear trend, but by the inherent randomness in the data. This serves as a transition into looking at statistical inference in linear models.
Sample Statistics versus Population¶
In this exercise we will work with a generated population. We will construct a sample by drawing points at random from the population. We will compute the mean standard deviation of the sample taken from that population to test whether the sample is representative of the population. Our goal is to see where the sample statistics are the same or very close to the population statistics.
Generate/Plot Data¶
sns.set(style="whitegrid", color_codes=True)
# Seed random number generator
np.random.seed(123)
population = np.random.normal(99.98, 9.73, 310)
sns.distplot(population, bins=25, color='r', kde=False);
# Compute the population statistics
print("Population mean {:.1f}, stdev {:.2f}".format(population.mean(), population.std()))
# Set random seed for reproducibility
np.random.seed(42)
# Construct a sample by randomly sampling 31 points from the population
sample = np.random.choice(population, size=31)
# Compare sample statistics to the population statistics
print("Sample mean {:.1f}, stdev {:.2f}".format(sample.mean(), sample.std()))
Notice that the sample statistics are similar to the population statistics, but not the identical. If you were to compute the len() of each array, it is very different, but the means are not that much different as you might expect.
Variation in Sample Statistics¶
If we create one sample of size=1000 by drawing that many points from a population. Then compute a sample statistic, such as the mean, a single value that summarizes the sample itself.
If you repeat that sampling process num_samples=100 times, you get $100$ samples. Computing the sample statistic, like the mean, for each of the different samples, will result in a distribution of values of the mean. The goal then is to compute the mean of the means and standard deviation of the means.
Here we will use population, num_samples, and num_pts, and note that the means and deviations arrays have been initialized to zero to give us containers to use for the for loop.
Generate/Plot Data¶
# Seed random number generator
np.random.seed(12)
population = np.random.normal(99.9840024355, 10.001880368, 1000000)
sns.distplot(population, bins=50, color='r', kde=False);
num_samples = 100
num_pts = 1000
# Initialize two arrays of zeros to be used as containers
means = np.zeros(num_samples)
stdevs = np.zeros(num_samples)
# For each iteration, compute and store the sample mean and sample stdev
for ns in range(num_samples):
sample = np.random.choice(population, num_pts)
means[ns] = sample.mean()
stdevs[ns] = sample.std()
# Compute and print the mean() and std() for the sample statistic distributions
print("Means: center={:>6.2f}, spread={:>6.2f}".format(means.mean(), means.std()))
print("Stdevs: center={:>6.2f}, spread={:>6.2f}".format(stdevs.mean(), stdevs.std()))
If we only took one sample, instead of $100$, there could be only a single mean and the standard deviation of that single value is zero. But each sample is different because of the randomness of the draws. The mean of the means is our estimate for the population mean, the stdev of the means is our measure of the uncertainty in our estimate of the population mean. This is the same concept as the standard error of the slope seen in linear regression.
Visualizing Variation of a Statistic¶
Previously, you have computed the variation of sample statistics. Now you'll visualize that variation.
We'll start with a preloaded population and a predefined function get_sample_statistics() to draw the samples, and return the sample statistics arrays.
def get_sample_statistics(population, num_samples=100, num_pts=1000):
means = np.zeros(num_samples)
deviations = np.zeros(num_samples)
for ns in range(num_samples):
sample = np.random.choice(population, num_pts)
means[ns] = sample.mean()
deviations[ns] = sample.std()
return means, deviations
# Generate sample distribution and associated statistics
means, stdevs = get_sample_statistics(population, num_samples=100, num_pts=1000)
# Define the binning for the histograms
mean_bins = np.linspace(97.5, 102.5, 51)
std_bins = np.linspace(7.5, 12.5, 51)
fig, ax = plt.subplots(nrows=1,ncols=2, figsize=(10,3))
sns.distplot(means, bins=mean_bins, color='g', kde=False, ax=ax[0])
sns.distplot(stdevs, bins=std_bins, color='r', kde=False, ax=ax[1])
ax[0].set_title(f'Distribution of the means:\n Center = {round(np.mean(means),2)}, Spread = {round(np.std(means),2)}')
ax[0].set_xlabel('Values of the means')
ax[0].set_ylabel('Bin counts of the means')
ax[1].set_title(f'Distribution of the Stdevs:\n Center = {round(np.mean(stdevs),2)}, Spread = {round(np.std(stdevs),2)}')
ax[1].set_xlabel('Values of the Stdevs')
ax[1].set_ylabel('Bin counts of the Stdevs')
plt.tight_layout();
Model Estimation and Likelihood¶
Likelihood vs Probability¶
- Probability
Probability is the measure of the likelihood that an event will occur. Representing the sample data distribution and probability being the area under the curve
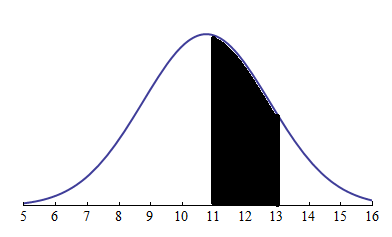
Likelihood
Likelihood is a function of parameters within the parameter space that describes the probability of obtaining the observed data. Likelihood being the point on the curve
Conditional Probability: $P$(outcome A∣given B)
- Probability: $P$(data∣model)
- Likelihood: $L$(model∣data)
Maximum likelihood estimation¶
In statistics, maximum likelihood estimation (MLE) is a method of estimating the parameters of a probability distribution by maximizing a likelihood function, so that under the assumed statistical model the observed data is most probable. The point in the parameter space that maximizes the likelihood function is called the maximum likelihood estimate.
Estimation of Population Parameters¶
Imagine a constellation ("population") of satellites orbiting for a full year, and the distance traveled in each hour is measured in kilometers. There is variation in the distances measured from hour-to-hour, due to unknown complications of orbital dynamics. Assume we cannot measure all the data for the year, but we wish to build a population model for the variations in orbital distance per hour (speed) based on a sample of measurements.
In this exercise, we will assume that the population of hourly distances are best modeled by a gaussian, and further assume that the parameters of that population model can be estimated from the sample statistics.
Generate/Plot Data¶
# Seed random number generator
np.random.seed(123)
sample_distances = np.random.normal(26918.3924141, 224.987088643, 1000)
sns.distplot(sample_distances, bins=50, color='r', kde=False);
def gaussian_model(x, mu, sigma):
return 1/(np.sqrt(2 * np.pi * sigma**2)) * np.exp( - (x - mu)**2 / (2 * sigma**2))
# Compute the mean and standard deviation of the sample_distances
sample_mean = np.mean(sample_distances)
sample_stdev = np.std(sample_distances)
# Use the sample mean and stdev as estimates of the population model parameters mu and sigma
population_model = gaussian_model(sample_distances, mu=sample_mean, sigma=sample_stdev)
# Plot the model and data to see how they compare
model_opts = dict(linewidth=4, color='red', alpha=0.5, linestyle=' ', marker="." )
data_opts = dict(color='grey', alpha=0.5)
y, x, _ = plt.hist(sample_distances, bins=30, label='data', normed=True, **data_opts)
# The histograms max pdf
scl = y.max()
# Normalized from 0 to the histograms max pdf
pop = scl*(population_model - np.min(population_model))/np.ptp(population_model)
plt.plot(sample_distances, pop, label='model', **model_opts)
plt.legend()
plt.tight_layout()
plt.show()
Notice in the plot that the data and the model do not line up exactly. This is to be expected because the sample is just a subset of the population, and any model built from it cannot be a prefect representation of the population. Also notice the vertical axis: it shows the normalize data bin counts, and the probability density of the model. Think of that as probability-per-bin, so that if summed all the bins, the total would be $1.0$.
Maximizing Likelihood, Part 1¶
Previously, we chose the sample mean as an estimate of the population model paramter mu. But how do we know that the sample mean is the best estimator? This is tricky, so let's do it in two parts.
In Part $1$, we will use a computational approach to compute the log-likelihood of a given estimate. Then, in Part $2$, we will see that when you compute the log-likelihood for many possible guess values of the estimate, one guess will result in the maximum likelihood.
# Compute sample mean and stdev, for use as model parameter guesses
mu_guess = np.mean(sample_distances)
sigma_guess = np.std(sample_distances)
# For each sample distance, compute the probability modeled by the parameter guesses
probs = np.zeros(len(sample_distances))
for n, distance in enumerate(sample_distances):
probs[n] = gaussian_model(distance, mu=mu_guess, sigma=sigma_guess)
# Compute the log-likelihood as the sum of the log(probs)
loglikelihood = np.sum(np.log(probs))
print('For guesses mu = {:0.2f} and sigma = {:0.2f}, the loglikelihood = {:0.2f}'.format(mu_guess, sigma_guess,
loglikelihood))
Although the likelihood (the product of the probabilities) is easier to interpret, the loglikelihood has better numerical properties. Products of small and large numbers can cause numerical artifacts, but sum of the logs usually doesnt suffer those same artifacts, and the "sum(log(things))" is closely related to the "product(things)"
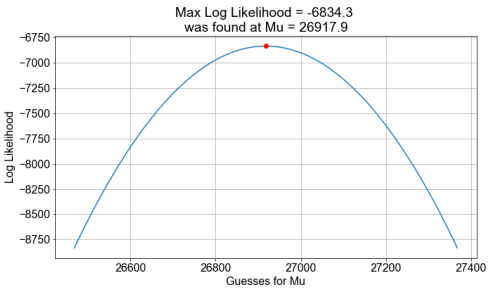
Maximizing Likelihood, Part 2¶
In Part $1$, we computed a single log-likelihood for a single mu. In this Part $2$, we will apply the predefined function compute_loglikelihood() to compute an array of log-likelihood values, one for each element in an array of possible mu values.
The goal then is to determine which single mu guess leads to the single maximum value of the loglikelihood array.
def compute_loglikelihood(samples, mu, sigma=250):
probs = np.zeros(len(samples))
for n, sample in enumerate(samples):
probs[n] = gaussian_model(sample, mu, sigma)
loglikelihood = np.sum(np.log(probs))
return loglikelihood
def plot_loglikelihoods(mu_guesses, loglikelihoods):
max_loglikelihood = np.max(loglikelihoods)
max_index = np.where(loglikelihoods==max_loglikelihood)
max_guess = mu_guesses[max_index][0]
font_options = {'family' : 'Arial', 'size' : 16}
plt.rc('font', **font_options)
fig, axis = plt.subplots(figsize=(8,4))
axis.plot(mu_guesses, loglikelihoods)
axis.plot(max_guess, max_loglikelihood, marker="o", color="red")
axis.grid()
axis.set_ylabel('Log Likelihoods')
axis.set_xlabel('Guesses for Mu')
axis.set_title('Max Log Likelihood = {:0.1f} \n was found at Mu = {:0.1f}'.format(max_loglikelihood,
max_guess))
fig.tight_layout()
plt.grid(True)
plt.show()
return fig
# Calulate sample mean and standard deviation
sample_mean = np.mean(sample_distances)
sample_stdev = np.std(sample_distances)
# Create an array of mu guesses, centered on sample_mean, spread out +/- by sample_stdev
low_guess = sample_mean - 2*sample_stdev
high_guess = sample_mean + 2*sample_stdev
mu_guesses = np.linspace(low_guess, high_guess, 101)
# Compute the loglikelihood for each model created from each guess value
loglikelihoods = np.zeros(len(mu_guesses))
for n, mu_guess in enumerate(mu_guesses):
loglikelihoods[n] = compute_loglikelihood(sample_distances, mu=mu_guess, sigma=sample_stdev)
# Find the best guess by using logical indexing, the print and plot the result
best_mu = mu_guesses[loglikelihoods==np.max(loglikelihoods)]
print(f'Maximum loglikelihood found for best mu guess = {best_mu[0]}')
fig = plot_loglikelihoods(mu_guesses, loglikelihoods)
Notice that the guess for mu that gave the maximum likelihood is precisely the same value as the sample.mean(). The sample_mean is thus said to be the "Maximum Likelihood Estimator" of the population mean mu. We call that value of mu the "Maximum Likelihood Estimator" of the population mu because, of all the mu values tested, it results in a model population with the greatest likelihood of producing the sample data we have.
Bootstrap and Standard Error¶
Imagine a National Park where park rangers hike each day as part of maintaining the park trails. They don't always take the same path, but they do record their final distance and time. We'd like to build a statistical model of the variations in daily distance traveled from a limited sample of data from one ranger.
Our goal is to use bootstrap resampling, computing one mean for each resample, to create a distribution of means, and then compute standard error as a way to quantify the "uncertainty" in the sample statistic as an estimator for the population statistic.
Generate/Plot Data¶
# Seed random number generator
np.random.seed(123)
sample_data = np.random.normal(5.01171255768, 3.52369839437, 500)
sns.distplot(sample_data, bins=30, color='r', kde=False);
def plot_data_hist(y):
font_options = {'family' : 'Arial', 'size' : 16}
plt.rc('font', **font_options)
fig, axis = plt.subplots(figsize=(8,4))
data_opts = dict(rwidth=0.8, color='blue', alpha=0.5)
bin_range = np.max(y) - np.min(y)
bin_edges = np.linspace(np.min(y), np.max(y), 21)
plt.hist(y, bins=bin_edges, **data_opts)
axis.set_xlim(np.min(y) - 0.5*bin_range, np.max(y) + 0.5*bin_range)
axis.grid("on")
axis.set_ylabel("Resample Counts per Bin")
axis.set_xlabel("Resample Means")
axis.set_title("Resample Count = {}, \nMean = {:0.2f}, Std Error = {:0.2f}".format(len(y), np.mean(y),
np.std(y)))
fig.tight_layout()
plt.show()
return fig
num_resamples = 100
resample_size = 500
bootstrap_means = np.zeros(num_resamples)
# Use the sample_data as a model for the population
population_model = sample_data.copy()
# Resample the population_model 100 times, computing the mean each sample
for nr in range(num_resamples):
bootstrap_sample = np.random.choice(population_model, size=resample_size, replace=True)
bootstrap_means[nr] = np.mean(bootstrap_sample)
# Compute and print the mean, stdev of the resample distribution of means
distribution_mean = np.mean(bootstrap_means)
standard_error = np.std(bootstrap_means)
print('Bootstrap Distribution: center={:0.1f}, spread={:0.1f}'.format(distribution_mean, standard_error))
# Plot the bootstrap resample distribution of means
fig = plot_data_hist(bootstrap_means)
Notice that standard_error is just one measure of spread of the distribution of bootstrap resample means.
Estimating Speed and Confidence¶
Let's look at the National Park hiking data. In this exercise, our goal is to use boot-strap resampling to find the distribution of speed values for a linear model, and then from that distribution, compute the best estimate for the speed and the $90$th percent confidence interval of that estimate. The speed here is the slope parameter from the linear regression model to fit distance as a function of time.
Load Data¶
fpath_csv = 'https://assets.datacamp.com/production/repositories/1480/datasets/2a0748a53d9f54544d63e451318b44cf438c01c2/hiking_data.csv'
df = pd.read_csv(fpath_csv, comment='#')
df.info()
distances = df['distance']
times = df['time']
Plot Data¶
plt.figure(figsize=(10,5))
plt.scatter(times, distances, s=5)
plt.grid(True)
plt.xlim(-1,11)
plt.ylim(-10,30)
plt.title('summary')
plt.xlabel('Time (hours)')
plt.ylabel('Distance (miles)');
def least_squares(x, y):
x_mean = np.sum(x)/len(x)
y_mean = np.sum(y)/len(y)
x_dev = x - x_mean
y_dev = y - y_mean
a1 = np.sum(x_dev * y_dev) / np.sum( np.square(x_dev) )
a0 = y_mean - (a1 * x_mean)
return a0, a1
num_resamples = 1000
resample_speeds = np.zeros(num_resamples)
# Resample each preloaded population, and compute speed distribution
population_inds = np.arange(0, 99, dtype=int)
for nr in range(num_resamples):
sample_inds = np.random.choice(population_inds, size=100, replace=True)
sample_inds.sort()
sample_distances = distances[sample_inds]
sample_times = times[sample_inds]
a0, a1 = least_squares(sample_times, sample_distances)
resample_speeds[nr] = a1
# Compute effect size and confidence interval, and print
speed_estimate = np.mean(resample_speeds)
ci_90 = np.percentile(resample_speeds, [5, 95])
print('Speed Estimate = {:0.2f}, 90% Confidence Interval: {:0.2f}, {:0.2f} '.format(speed_estimate, ci_90[0],
ci_90[1]))
Notice that the speed estimate (the mean) falls inside the confidence interval (the $5$th and $95$th percentiles). Moreover, notice if you computed the standard error, it would also fit inside the confidence interval. Think of the standard error here as the 'one sigma' confidence interval. Note that this should be very similar to the summary output of a statsmodels ols() linear regression model, but here you can compute arbitrary percentiles because you have the entire speeds distribution.
Visualize the Bootstrap¶
Continuing where we left off previously, let's visualize the bootstrap distribution of speeds estimated using bootstrap resampling, where we computed a least-squares fit to the slope for every sample to test the variation or uncertainty in our slope estimation.
# Generate the speed sample distribution
def compute_resample_speeds(distances, times):
num_resamples = 1000
population_inds = np.arange(0, 99, dtype=int)
resample_speeds = np.zeros(num_resamples)
for nr in range(num_resamples):
sample_inds = np.random.choice(population_inds, size=100, replace=True)
sample_inds.sort()
sample_distances = distances[sample_inds]
sample_times = times[sample_inds]
a0, a1 = least_squares(sample_times, sample_distances)
resample_speeds[nr] = a1
return resample_speeds
# Create the bootstrap distribution of speeds
resample_speeds = compute_resample_speeds(distances, times)
speed_estimate = np.mean(resample_speeds)
percentiles = np.percentile(resample_speeds, [5, 95])
# Plot the histogram with the estimate and confidence interval
fig, axis = plt.subplots()
axis.hist(resample_speeds, bins=30, color='green', alpha=0.35, rwidth=0.9)
axis.axvline(speed_estimate, label='Estimate', color='r')
axis.axvline(percentiles[0], label=' 5th', color='b', linestyle='--')
axis.axvline(percentiles[1], label='95th', color='b', linestyle='--')
plt.title(f'90% Confidence Interval {round(percentiles[0],2)}, {round(percentiles[1],2)}')
axis.legend()
plt.show()
Notice that vertical lines marking the $5$th (left) and $95$th (right) percentiles mark the extent of the confidence interval, while the speed estimate (center line) is the mean of the distribution and falls between them. Note the speed estimate is the mean, not the median, which would be $50\%$ percentile.
Test Statistics and Effect Size¶
How can we explore linear relationships with bootstrap resampling? Back to the trail! For each hike plotted as one point, we can see that there is a linear relationship between total distance traveled and time elapsed. It we treat the distance traveled as an "effect" of time elapsed, then we can explore the underlying connection between linear regression and statistical inference.
In this exercise, you will separate the data into two populations, or "categories": early times and late times. Then you will look at the differences between the total distance traveled within each population. This difference will serve as a "test statistic", and it's distribution will test the effect of separating distances by times.
Plot Data¶
plt.figure(figsize=(10,5))
col = np.where(np.array(times)<5,'r','b')
plt.scatter(times, distances, s=5, c=col)
plt.grid(True)
plt.title('summary')
plt.xlabel('Time (hours)')
plt.ylabel('Distance (miles)');
def plot_test_statistic(test_statistic):
"""
Purpose: Plot the test statistic array as a histogram
Args:
test_statistic (np.array): an array of test statistic values, e.g. resample2 - resample1
Returns:
fig (plt.figure): matplotlib figure object
"""
t_mean = np.mean(test_statistic)
t_std = np.std(test_statistic)
t_min = np.min(test_statistic)
t_max = np.max(test_statistic)
bin_edges = np.linspace(t_min, t_max, 21)
data_opts = dict(rwidth=0.9, color='blue', alpha=0.5)
fig, axis = plt.subplots(figsize=(8,4))
plt.hist(test_statistic, bins=bin_edges, **data_opts)
axis.grid()
axis.set_ylabel("Bin Counts")
axis.set_xlabel("Distance Differences, late - early")
title_form = "Test Statistic Distribution, \nMean = {:0.2f}, Std Error = {:0.2f}"
axis.set_title(title_form.format(t_mean, t_std))
plt.grid(True)
plt.show()
return fig
sample_distances = df['distance'].values
sample_times = df['time'].values
# Create two poulations, sample_distances for early and late sample_times.
# Then resample with replacement, taking 500 random draws from each population.
group_duration_short = sample_distances[sample_times < 5]
group_duration_long = sample_distances[sample_times > 5]
resample_short = np.random.choice(group_duration_short, size=500, replace=True)
resample_long = np.random.choice(group_duration_long, size=500, replace=True)
# Difference the resamples to compute a test statistic distribution, then compute its mean and stdev
test_statistic = resample_long - resample_short
effect_size = np.mean(test_statistic)
standard_error = np.std(test_statistic)
# Print and plot the results
print('Test Statistic: mean={:0.2f}, stdev={:0.2f}'.format(effect_size, standard_error))
fig = plot_test_statistic(test_statistic)
Notice again, the test statistic is the difference between a distance drawn from short duration trips and one drawn from long duration trips. The distribution of difference values is built up from differencing each point in the early time range with one from the late time range. The mean of the test statistic is not zero and tells us that there is on average a difference in distance traveled when comparing short and long duration trips. Again, we call this the 'effect size'. The time increase had an effect on distance traveled. The standard error of the test statistic distribution is not zero, so there is some spread in that distribution, or put another way, uncertainty in the size of the effect.
Null Hypothesis¶
In this exercise, we formulate the null hypothesis as
short and long time durations have no effect on total distance traveled.
We interpret the "zero effect size" to mean that if we shuffled samples between short and long times, so that two new samples each have a mix of short and long duration trips, and then compute the test statistic, on average it will be zero.
In this exercise, our goal is to perform the shuffling and resampling. Start with the predefined group_duration_short and group_duration_long which are the un-shuffled time duration groups.
# Shuffle the time-ordered distances, then slice the result into two populations.
shuffle_bucket = np.concatenate((group_duration_short, group_duration_long))
np.random.shuffle(shuffle_bucket)
slice_index = len(shuffle_bucket)//2
shuffled_half1 = shuffle_bucket[0:slice_index]
shuffled_half2 = shuffle_bucket[slice_index:]
# Create new samples from each shuffled population, and compute the test statistic
resample_half1 = np.random.choice(shuffled_half1, size=500, replace=True)
resample_half2 = np.random.choice(shuffled_half2, size=500, replace=True)
test_statistic = resample_half2 - resample_half1
# Compute and print the effect size
effect_size = np.mean(test_statistic)
print('Test Statistic, after shuffling, mean = {}'.format(effect_size))
Notice that your effect size is not exactly zero because there is noise in the data. But the effect size is much closer to zero than before shuffling. Notice that if you rerun your code, which will generate a new shuffle, you will get slightly different results each time for the effect size, but np.abs(test_statistic) should be less than about $1.0$, due to the noise, as opposed to the slope, which was about $2.0$
Visualizing Test Statistics¶
In this exercise, we will approach the null hypothesis by comparing the distribution of a test statistic arrived at from two different ways.
First, we will examine two "populations", grouped by early and late times, and computing the test statistic distribution. Second, shuffle the two populations, so the data is no longer time ordered, and each has a mix of early and late times, and then recompute the test statistic distribution.
def shuffle_and_split(sample1, sample2):
shuffled = np.concatenate((sample1, sample2))
np.random.shuffle( shuffled )
half_length = len(shuffled)//2
sample1 = shuffled[0:half_length]
sample2 = shuffled[half_length+1:]
return sample1, sample2
def plot_test_statistic(test_statistic, label=''):
"""
Purpose: Plot the test statistic array as a histogram
Args:
test_statistic (np.array): an array of test statistic values, e.g. resample2 - resample1
Returns:
fig (plt.figure): matplotlib figure object
"""
t_mean = np.mean(test_statistic)
t_std = np.std(test_statistic)
t_min = np.min(test_statistic)
t_max = np.max(test_statistic)
#bin_edges = np.linspace(t_min, t_max, 21)
bin_edges = np.linspace(-25, 25, 51)
data_opts = dict(rwidth=0.9, color='blue', alpha=0.5)
fig, axis = plt.subplots(figsize=(8,4))
plt.hist(test_statistic, bins=bin_edges, **data_opts)
axis.grid()
axis.set_ylim(-5, +55)
axis.set_xlim(-25, +25)
axis.set_ylabel("Bin Counts")
axis.set_xlabel("Test Statistic Values".format(label))
title_form = "{} Groups: Test Statistic Distribution, \nMean = {:0.2f}, Std Error = {:0.2f}"
axis.set_title(title_form.format(label, t_mean, t_std))
plt.grid(True)
plt.show()
return fig
# From the unshuffled populations, compute the test statistic distribution
resample_short = np.random.choice(group_duration_short, size=500, replace=True)
resample_long = np.random.choice(group_duration_long, size=500, replace=True)
test_statistic_unshuffled = resample_long - resample_short
# Shuffle two populations, cut in half, and recompute the test statistic
shuffled_half1, shuffled_half2 = shuffle_and_split(group_duration_short, group_duration_long)
resample_half1 = np.random.choice(shuffled_half1, size=500, replace=True)
resample_half2 = np.random.choice(shuffled_half2, size=500, replace=True)
test_statistic_shuffled = resample_half2 - resample_half1
# Plot both the unshuffled and shuffled results and compare
fig = plot_test_statistic(test_statistic_unshuffled, label='Unshuffled')
fig = plot_test_statistic(test_statistic_shuffled, label='Shuffled')
Notice that after you shuffle, the effect size went almost to zero and the spread increased, as measured by the standard deviation of the sample statistic, aka the 'standard error'. So shuffling did indeed have an effect. The null hypothesis is disproven. Time ordering does in fact have a non-zero effect on distance traveled. Distance is correlated to time.
Visualizing the P-Value¶
In this exercise, you will visualize the p-value, the chance that the effect (or "speed") we estimated, was the result of random variation in the sample. Your goal is to visualize this as the fraction of points in the shuffled test statistic distribution that fall to the right of the mean of the test statistic ("effect size") computed from the unshuffled samples.
def compute_test_statistic(sample1, sample2):
resample1 = np.random.choice(sample1, size=500, replace=True)
resample2 = np.random.choice(sample2, size=500, replace=True)
test_statistic = resample2 - resample1
return test_statistic
def plot_test_stats_and_pvalue(test_statistic, shuffle_statistic):
"""
Purpose: Plot the test statistic array as a histogram
Args:
test_statistic (np.array): an array of test statistic values, e.g. resample2 - resample1
shuffle_statistic (np.array): an array of test statistic values, from shuffled resamples
Returns:
fig (plt.figure): matplotlib figure object
"""
t_mean = np.mean(test_statistic)
t_std = np.std(test_statistic)
t_min = np.min(test_statistic)
t_max = np.max(test_statistic)
effect_size = np.mean(test_statistic)
p_value = len(shuffle_statistic[shuffle_statistic>=effect_size])/len(shuffle_statistic)
#bin_edges = np.linspace(t_min, t_max, 21)
bin_edges = np.linspace(-25, 25, 51)
shuffle_opts = dict(rwidth=0.9, color='blue', alpha=0.35, label='Shuffled')
test_opts = dict(rwidth=0.9, color='red', alpha=0.35, label='Unshuffled')
fig, axis = plt.subplots(figsize=(8,4))
plt.hist(test_statistic, bins=bin_edges, **test_opts)
plt.hist(shuffle_statistic, bins=bin_edges, **shuffle_opts)
axis.axvline(effect_size, color='black', label='Effect Size')
axis.axvspan(effect_size, +25, alpha=0.10, color='black', label='p-value')
axis.grid()
#axis.set_ylim(-5, +55)
axis.set_xlim(-25, +25)
axis.set_ylabel("Bin Counts")
axis.set_xlabel("Test Statistic Values")
title_form = ("Test Statistic Distibution, \n"
"Effect Size = {:0.2f}, p-value = {:0.02f}")
axis.set_title(title_form.format(effect_size, p_value))
axis.legend(loc='upper left')
plt.grid(True)
plt.show()
return fig
# Compute the test stat distribution and effect size for two population groups
test_statistic_unshuffled = compute_test_statistic(group_duration_short, group_duration_long)
effect_size = np.mean(test_statistic_unshuffled)
# Randomize the two populations, and recompute the test stat distribution
shuffled_half1, shuffled_half2 = shuffle_and_split(group_duration_short, group_duration_long)
test_statistic_shuffled = compute_test_statistic(shuffled_half1, shuffled_half2)
# Compute the p-value as the proportion of shuffled test stat values >= the effect size
condition = test_statistic_shuffled >= effect_size
p_value = len(test_statistic_shuffled[condition]) / len(test_statistic_shuffled)
# Print p-value and overplot the shuffled and unshuffled test statistic distributions
print("The p-value is = {}".format(p_value))
fig = plot_test_stats_and_pvalue(test_statistic_unshuffled, test_statistic_shuffled)
There is a $13\%$ chance to get a speed of $10$ or more due to random chance.
- Note that if we divide these distance differences by the by the time differences the test statistic becomes the speed or an estimate for the slop parameter in a linear model.
- Also note that the entire point of this is compute a p-value to quantify the chance that our estimate for speed could have been obtained by random chance. On the plot, the unshuffle test stats are the distribution of speed values estimated from time-ordered distances. The shuffled test stats are the distribution of speed values computed from randomizing unordered distances. Values of the shuffled stats to the right of the mean non-shuffled effect size line are those that both ($1$) could have both occured randomly and ($2$) are at least as big as the estimate you want to use for speed.